GAMES-101

前言

最近在研读LearnOpenGL过程中感觉对一些概念性内容还不是很了解，便询问了图形学专业的室友，问问还有没有什么可以学习的资料，于是乎便有了此篇

本笔记来源于 UCSB 闫令琪老师 的 GAMES01-现代计算机图形学入门

Overview

图形学在电影、游戏、设计中被广泛应用，此外还在可视化（医学、统计学）、VR、模拟、GUI等领域大展身手

计算机图形学的范畴中，实时的定义是每秒要生成30个画面，否则就称之为离线

本课程涵盖的问题

• Rasterization 光栅化
• Curves and Meshes 如何表示曲线
• Ray Tracing 光线追踪
• Animation / Simulation 动画以及仿真

计算机图形学与计算机视觉的区别

一切需要猜测的，属于计算机视觉

Review Linear Algebra

图形学依赖于线性代数

具体内容不从头铺开，这里进行查漏补缺

向量

向量 表示两个不同方向的内容，方向以及长度

默认地，用列来表示向量

单位向量计算，注意单位向量$\hat{\mathbf{v}}$ 称为v-hat

$$\hat{\mathbf{v}}=\frac{\mathbf{v}}{|\mathbf{v}|}$$

向量的点乘和叉乘

点乘的几何意义

点乘的性质（交换律、结合律、分配律）

应用：快速得到两个向量之间的夹角，判断两个向量方向是否接近，光照计算，向量投影

叉乘的几何意义

叉乘的性质（结合律、分配律）

右手三指定则与右手螺旋定则都能进行叉乘方向判断

作用：建立三维空间坐标系，判断左与右、内与外

矩阵

图形学中，矩阵最大的作用是变换

矩阵乘积

矩阵相乘的性质（结合律、分配律）

矩阵转置、互逆矩阵

向量的点乘叉乘都可以写为矩阵相乘的形式

Transformation

二维变换

不同的变换

变换的作用？

Transformation可以分为两类：

• Modeling：Translation、Rotating、Scaling
• Viewing：Projection(3D to 2D)

二维空间上如何进行Scaling？

要理解以下方程的数学意义以及几何意义

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}{s}_0& 0\\ 0& s_1\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$$

一些不同类型的变换：

Scaling缩放、Reflection镜像翻转、Shear切变、Rotate旋转

以上操作都是线性变换。

什么是线性变换？线性变换有什么性质？

线性变换

描述在向量空间中的一种变换方式。一个变换 T 是线性变换，它必须满足以下性质

• 加法保持性 $T(\mathbf{u}+\mathbf{v})=T(\mathbf{u})+T(\mathbf{v})$
• 数乘保持性 $T(c\mathbf{v})=cT(\mathbf{v})$

但为什么没有平移操作？Translation平移操作为什么特殊？为什么平移变换不是线性变换？是否有一种方式来统一所有的变换？

平移后需改写为以下形式：

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]+\left[\begin{array}{c}{t}_x\\ t_y\end{array}\right]$$

齐次坐标

核心是升维，目的是统一变换的实现方式

• 对于2D坐标, 升维后为$(x,y,1{)}^T$
• 对于2D向量，升维后为$(x,y,0{)}^T$。此时，平移操作不会改变向量的值(因为按照向量的性质，平移后的向量与原向量相等，我们不希望结果不变)

Validation

为什么这种方式升维是有效的？

尝试将以上齐次坐标下点和向量的定义(额外维度的0或1)带入，验证不同加减场景

• 向量 + 向量 = 向量
• 点 - 点 = 向量
• 点 + 向量 = 点 (代表该点沿着某个向量移动)
• 点 + 点 = 点 (但需要进行一些额外操作，实际代表的是这两个点的重点，因为根据定义，在齐次坐标系中$
  \begin{bmatrix}
  x \
  y \
  w
  \end{bmatrix} $ 实际代表的是2D坐标系中的$\left[\begin{array}{c}\frac{x}{w}\\ \frac{y}{w}\\ 1\end{array}\right]$)

终极意义

因此，我们就能用以下的方式来表示平移操作

$$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ w^{\prime }\end{array}\right]=\left[\begin{array}{ccc}1& 0& t_x\\ 0& 1& t_y\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ 1\end{array}\right]=\left[\begin{array}{c}x+t_x\\ y+t_y\\ 1\end{array}\right]$$

当然也能用这种方式来表示所有变换操作

我们将包含平移变换的诸多变换称为仿射变换（Affine Transformation），它是保持直线性和比例关系的变换，它是比线性变换更一般的变换

$${\mathbf{x}}^{\prime }=A\mathbf{x}+\mathbf{b}$$

复合变换

矩阵的乘法不具有交换性: 有先后次序的两个变换，交换变换次序后，最后的变换效果可能不一致

但矩阵乘法具有结合性，因此我们就有了复合矩阵

$$A_n(\dots A_2(A_1(x)))=(A_n\cdots A_2\cdot A_1)\cdot \left[\begin{array}{c}x\\ y\\ z\end{array}\right]=A^{\prime }\cdot \left[\begin{array}{c}x\\ y\\ z\end{array}\right]$$

因此，我们可以使用一个矩阵来表示一个复合变换

矩阵为什么具有结合性？

这里也比较有意思，建议从几何和数学角度推导，需要用到求和符号的性质～

三维变换

三维旋转

三维坐标下的二维旋转

绕不同坐标轴(正方向，逆时针)旋转 $\alpha$ 度时的变换矩阵

$$\begin{gathered} {\mathbf{R}}_x(\alpha )=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& \cos \alpha & -\sin \alpha & 0\\ 0& \sin \alpha & \cos \alpha & 0\\ 0& 0& 0& 1\end{array}\right) \\ {\mathbf{R}}_y(\alpha )=\left(\begin{array}{cccc}\cos \alpha & 0& \sin \alpha & 0\\ 0& 1& 0& 0\\ -\sin \alpha & 0& \cos \alpha & 0\\ 0& 0& 0& 1\end{array}\right) \\ {\mathbf{R}}_z(\alpha )=\left(\begin{array}{cccc}\cos \alpha & -\sin \alpha & 0& 0\\ \sin \alpha & \cos \alpha & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right) \end{gathered}$$

:::important需要注意的是，为什么Y轴这里不一样？

自己试下如果是xzy轴是否还满足右手定则？应该是zxy轴满足右手定则， 实际旋转角度应该是z轴->x轴，用二维计算坐标方式代入计算即可求得该式子。奇怪的原因是x轴与z轴对调了。可以自己草稿推演一下～

:::

三维旋转

复合的旋转操作都可以分解为绕xyz轴进行不同的旋转

$${\mathbf{R}}_{xyz}(\alpha ,\beta ,\gamma )={\mathbf{R}}_x(\alpha ){\mathbf{R}}_y(\beta ){\mathbf{R}}_z(\gamma )$$

借助飞机的模型，引入欧拉角的概念，来解决三维空间中所有可能的旋转情况

• Pitch: 俯仰角，绕z轴旋转
• Yaw: 偏移角，绕y轴旋转
• Roll：翻滚角，绕x轴旋转

Rodrigues’ Rotation Formula 罗德里格旋转公式：计算3D坐标下的旋转矩阵（绕任意的旋转轴旋转任意角度）

视图变化

视图变化又称为摄像机变化，View / Camera Transformation ，处理的是将看到的3维物体，转化为而二维图片，就好比摄像机拍了一张照片一样。

学完这一部分，我觉得你将为大自然中眼球和大脑工作机制的神秘和美而惊叹

如何表示一个相机位置？

在图形学中，默认地我们会认为相机始终处于原点，并且以Y轴作为上方向，望向Z轴负方向

因此，在空间中添加一个摄像机并准备以此摄像机为基准观测物体时，我们就需要做一系列的变换，将相机从起始点移动到原点并修正其朝向（但实际我们移动到是整体场景），如何进行转化呢？

假设摄像机位于(x, y, z)点，通常我们会这么做：平移 + 旋转

平移

将摄像机从目标点先移动到原点

$${\mathbf{T}}_{\text{translate}}=\left(\begin{array}{cccc}1& 0& 0& -x\\ 0& 1& 0& -y\\ 0& 0& 1& -z\\ 0& 0& 0& 1\end{array}\right)$$

旋转

将摄像机移动到原点后，我们还需要旋转其方向，或者说匹配坐标轴与基准坐标轴。

• 修正摄像机朝向，将摄像机观测方向旋转到Z轴负方向
• 修正上朝向，将摄像机上方向旋转到Y轴
• 修正右方向，将摄像机右方向旋转到X轴

如果将某一个向量旋转到与坐标轴相同，我们会觉得困难，但如果反过来考虑，将某一坐标轴旋转到指定位置，就非常好写

假设原来摄像机的方向向量、上向量为 $\hat{g} \ ,\ \hat{t} $,\mathrm{其}\mathrm{右}\mathrm{向}\mathrm{量}\mathrm{自}\mathrm{然}\mathrm{为}\mathrm{为}$\hat{g} \times \hat{t}$

$$R_{view}^{-1}=\left[\begin{array}{cccc}{x}_{\hat{g}\times \hat{t}}& x_t& x_{-g}& 0\\ y_{\hat{g}\times \hat{t}}& y_t& y_{-g}& 0\\ z_{\hat{g}\times \hat{t}}& z_t& z_{-g}& 0\\ 0& 0& 0& 1\end{array}\right]$$

因此，我们需要求得该矩阵的逆矩阵，而这又是一个旋转矩阵，对于旋转矩阵，其逆就位该矩阵的转置矩阵，为什么呢？这涉及到线性代数的知识，我们马上会讨论到

$$R_{view}=\left[\begin{array}{cccc}{x}_{\hat{g}\times \hat{t}}& y_{\hat{g}\times \hat{t}}& z_{\hat{g}\times \hat{t}}& 0\\ x_t& y_t& z_t& 0\\ x_{-g}& y_{-g}& z_{-g}& 0\\ 0& 0& 0& 1\end{array}\right]$$

正交矩阵Orthogonal Matrix

这里需要回顾下正交矩阵的概念

当矩阵的逆矩阵等于该矩阵的转置矩阵时，这个矩阵被称为正交矩阵，即：$A^{-1}=A^T$

从几何的概念理解正交矩阵：绕某个轴旋转 $\theta$ 角与旋转 $-\theta$ 角，则这两次变换的矩阵就为正交矩阵，因为$A_{\theta }{A}_{-\theta }=I$, 这在几何上是合理的，因为最终的结果是物体位置没有发生变化。$A_{\theta }$ 与 $A_{-\theta }$互为逆矩阵

关键性质

• 行/列 向量是单位向量且两两正交(点积为0) $||{\mathbf{u}}_i||=1$ && ${\mathbf{u}}_i\cdot {\mathbf{u}}_j=0,i\ne j$
• 行列式的值为1或-1

可以发现这些关键性质与坐标轴的性质似乎天生匹配。

推导

$$(A^{T}A{)}_{ij}=\{\begin{array}{l}{\mathbf{u}}_i{\mathbf{u}}_j=0,i\ne j\\ {\mathbf{u}}_i{\mathbf{u}}_j=1,i=j\end{array}$$

因此最终的变换矩阵就为，注意顺序，我们是先移动坐标再旋转

$$A_{final}=R_{view}{T}_{translate}$$

投影变化

投影的作用是什么？如何让二维图片看起来真实

很喜欢这样的一句解释，投影其实是将高维数据投影到低纬数据的一种方式，在这个过程中，必将存在一些高维数据在降维时引发的数据丢失问题。不同的投影有不同的数据丢失情况，有不同的使用场景

投影的标准定义

给定向量空间 V 和其子空间 W ，投影变换 P 是一个 线性变换，$P:V\to W$，使得

1. 投影结果均处于子空间内 $P(\mathbf{v})\in W$
2. 投影后的向量在投影空间内保持不变 $P(\mathbf{w})=\mathbf{w}$
3. 投影应用两次与应用一次相同（幂等性） $P^2=P$

3维空间中，我们常比做将空间中的长方体，映射为canonical cube, 即中心在原点且各轴范围均为[-1, 1]的正方体。

image

正交投影 Orthographic

同样地，给出如下定义

给定一个向量空间 $V$ 和其子空间 $W\subseteq V$，将向量 $\mathbf{v}\in V$ 投影到 $W$ 的变换 $P$ 称为 正交投影，当且仅当满足以下条件

• 投影结果在子空间内：$P(\mathbf{v})\in W$ (投影本身就具有的性质)
• 投影误差与投影面正交：$\mathbf{v}-P(\mathbf{v})\perp W$ (特性)
• 幂等性：$P^2=P$ (投影本身就具有的性质)
• 正交性：$P=P^T$

定义上其实是有点不好理解的，这里用Wiki的解释来理解下～

:::detail From Wiki

正交投影是一种平行投影，所有投射线都与投影平面垂直，导致场景的每个平面都以仿射变换的形式出现在观察表面上。

:::

大致可以理解为假设相机离得无限远，在原有摄像机坐标系基础下，丢掉Z轴，并映射为[-1, 1]的区间内

这里需要进行平移和缩放两步，其中 r l t b n f 分别是其6个顶点，这里不过多赘述，可以自行画图推断～

$$M_{ortho}=\left[\begin{array}{cccc}\frac{2}{r-l}& 0& 0& 0\\ 0& \frac{2}{t-b}& 0& 0\\ 0& 0& \frac{2}{n-f}& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& -\frac{r+l}{2}\\ 0& 1& 0& -\frac{t+b}{2}\\ 0& 0& 1& -\frac{n+f}{2}\\ 0& 0& 0& 1\end{array}\right]$$

透视投影 Perspective

核心是与人眼光学一致，有近大远小的效果，更符合人眼（平行的可能不再平行），有兴趣可以先了解下人眼的结构以及人眼成像的原理。

undefined

需要提前了解一些概念，视锥体，近平面，远平面。

可以理解为，我们如何将远平面投影到近平面上

根据闫令琪老师的解释，可以理解为将远平面挤压成与近平面一致，然后再通过正交投影，投影到近平面。我们知道正交投影该怎么办了 ，但现在问题来了，我们该怎么挤？

这里由于光的直线性，我们可以借助相似三角形的知识来找到映射关系，这里具体的矩阵推导这里就不手动暂不展开了，难点在于如何推导z轴的变化。可以自行观看老师的视频推导～

假设我们进行的是将z = f的远平面内容投射到z = n的近平面(f < n)

$$M_{pers\to ortho}=\left[\begin{array}{cccc}n& 0& 0& 0\\ 0& n& 0& 0\\ 0& 0& n+f& -nf\\ 0& 0& 1& 0\end{array}\right]$$

带入之前的正交投影，我们就有最终的透视投影矩阵～建议自己借助闫令琪老师的课件推导下，看能不能推出来。

$$M_{per}=\left[\begin{array}{cccc}\frac{2n}{r-l}& 0& \frac{l+r}{l-r}& 0\\ 0& \frac{2n}{t-b}& \frac{b+t}{b-t}& 0\\ 0& 0& \frac{f+n}{n-f}& \frac{2fn}{f-n}\\ 0& 0& 1& 0\end{array}\right]$$

可以给近平面定义一个宽度高度并定义一个宽高比aspect: width / height

并在定义一个概念：视角（Field Of View），表示可以看到的角度的范围（垂直可视角度）

Wiki-FOV

即上图中中间部分与摄像机所称的夹角，所以就有

$$\begin{gathered} \tan \frac{fovY}{2}=\frac{t}{|n|} \\ \text{aspect}=\frac{r}{t} \end{gathered}$$

这是gpt给出的标准透视投影矩阵, 有空可以后续研究

$$M_{perspective}=\left[\begin{array}{cccc}\frac{1}{\text{aspect}\cdot \tan (\frac{\text{fov}}{2})}& 0& 0& 0\\ 0& \frac{1}{\tan (\frac{\text{fov}}{2})}& 0& 0\\ 0& 0& -\frac{f+n}{f-n}& -\frac{2fn}{f-n}\\ 0& 0& -1& 0\end{array}\right]$$

参数	含义
fov	Field of View：垂直视场角，控制视锥体张开的角度，通常为 45°。
aspect	Aspect Ratio：纵横比，通常为 屏幕宽度 / 屏幕高度，防止画面变形。
n (near)	近平面：离摄像机最近的可见距离，必须为正值。
f (far)	远平面：离摄像机最远的可见距离，通常比 near 大得多。
$\tan \left(\frac{\text{fov}}{2}\right)$	通过三角函数控制视锥体的开口大小。

Rasterization 光栅化

在进行完投影后，我们就得到了一个包含部分三维信息的二维平面，接下来的问题是如何将这个标准化的二维平面的数据 “渲染” 到屏幕上。我们的目标是将这个标准化二维平面的点 转化为 连续的图形

基本

学习这部分内容时请先了解 像素、分辨率、1080P等概念。

光栅化是什么

Rasterize 光栅化，即将物体画在屏幕上的过程。

Pixel 像素（Picture Element）： a little square with uniform color (mixture of RGB).

目前可以粗浅地理解为像素是屏幕上颜色绘制的最小单位

实践中，用坐标化的方式来表示像素左下角位置(实际中心还需要在(x, y)基础上进行一定偏移)。由于屏幕被像素占据满，因此屏幕也可进行坐标化。规定是屏幕的范围是(0, 0) -> (width, height)，注意，屏幕的坐标没有负值，从左下角都右上角

目前我们有一个[-1, 1]的二维平面，我们需要将其映射到[width, height]的屏幕上，因此我们需要进行坐标放缩处理，并移动中心，因为屏幕没有负的坐标轴。因此我们有变化矩阵：

$$M_{viewport}=\left(\begin{array}{cccc}\frac{\text{width}}{2}& 0& 0& \frac{\text{width}}{2}\\ 0& \frac{\text{height}}{2}& 0& \frac{\text{height}}{2}\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)$$

早期显示屏

谈到了显示相关的知识，那就来了解了解电子显示器的历史吧～

这里我参考了以下视频，受益匪浅

• 【硬核科普】全网最简洁易懂的OLED与LCD屏幕工作原理与优劣科普
• 【中字】慢镜头下的电视工作原理科普（CRT/LED/OLED)

早期的光栅显示设备：CRT 显像管设备（比如示波器，大学物理做实验用到过）是如何进行显示的呢？

CRT(Cathode Ray Tube)显像管

由电子枪与偏转线圈组成，以极快地速度射出电子束并控制电子射出后的落点位置，通过扫描的方式（按行扫描， 每行中从左至右）显示。

CRT Structure

屏幕上涂有荧光粉，荧光材料吸收电子能量，激发电子跃迁，释放光子，形成可见光（不同材质的荧光粉释放光子时可能产生不同的颜色）。当电子以高速撞击荧光粉时，部分动能转移到荧光粉原子中的电子，被激发的电子吸收能量，跃迁至更高能级（激发态），但激发状态的电子不稳定，会自发回到基态，在返回基态的过程中，会以光子形式释放能量。电子束离开后，荧光粉不会立即停止发光，而是经历余辉过程，通常在1ms至几十ms之间消失，这是因为某些电子被捕获在陷阱能级，延迟释放光子。

CRT屏幕上，只显示激活状态的像素扫描线，但由于其扫描频率十分快、人眼的视觉残留效应、以及荧光粉瞬时发光后的余辉效果，还是会显示出以前的图像，使得屏幕整体显示出一副完整的画面。且由于早期电缆传输的信号十分有限，早期电视通常使用隔行扫描的方式

Scan

隔行扫描i、逐行扫描p的区别是什么？

历史来源：早期电缆传输的信号十分有限，因此通常把一帧图像按像素行拆分为两部分，称为两个场，奇场和偶场。

隔行扫描 i：通过奇数行、偶数行规则将连续两帧画面通过两场扫描而成，即对于第一帧只扫描奇数行，对于第二帧只扫描偶数行。这样对于每帧，实际只用到了一半的数据。

逐行扫描 P：不区分场的概念，直接完整地逐行进行扫描，或者说发射电子束。

	优点	缺点
隔行扫描	节省带宽	1. 清晰度下降 2. 快速运动时，奇偶场内容差异大，会导致画面撕裂，出现锯齿状或者拉丝效应
逐行扫描	画面流畅无撕裂	带宽要求高

因此我们现代常说的1080P代表的意思就是逐行扫描

目前随着带宽能力的提高，大部分电视以及显示器都是逐行扫描～

现代屏幕的显示方式

通过将内存（显存）中的数据传递给显示器

现代的显示设备：LCD、LED、OLED、墨水屏（Electronic Ink Display）

现代显示屏

LCD (Liquid Crystal Display)

组成：背光层、液晶层、滤光层

每个像素由RGB三个子像素组成，实际对应的是不同的纯色元件。实际显示时，每个像素点根据该点的颜色来调整三个纯色元件的色值来达到颜色显示的目的。

实际的工作流程，可以理解为，最底部的背光层(通常是一整块)从下至上发射白光，并通过控制液晶层与偏光片部分，来控制白光的通过比例，进而达到控制色值的目标

Structure

LED (Light-Emitting Diode)

发光二极管，LCD背光的改进，基础还是LCD面板技术

OLED (Oragnic Light-Emitting Diode)

OLED 即 有机发光二极管

与LCD类似，每个像素也由RGB三个子像素构成，但与LCD不同的是，它没有背光层与偏光片，每个小像素点本身是一种特殊设计的发光二极管，基于通电大小来控制亮度。每个小像素点都类似于是一个可以独立控制的灯柱，因此有以下好处。

低功耗下的熄屏显示

因此可以低功耗做Always On Display 熄屏提示，因为只需要一部分灯珠保持常亮即可，而LCD不能，因为其背部的背光板是一整片的，必须要先开启正片的背光板再调整偏光片和液晶层来控制每个像素的色值，因此做不到低功耗。

对比度高 & 无漏光

LCD无法显示纯黑色，因为其液晶分子无法完全闭合，因此会有部分白光透出，导致并非是纯黑的黑色。而OLED由于没有背光的存在，可以通过直接断掉供电来形成纯黑。

屏幕响应速度快

每个像素从一个颜色切换到另一个颜色需要一定时间，对于LCD而言，其切换是通过控制液晶层偏转完成，但其与温度有关，温度越低偏转越慢，因此在低温下，LCD屏幕就会因来不及改变颜色而出现残影。而OLED由于本身就没有液晶层，所以不受温度限制，因此在显示动态画面上，OLED是天生就具有优势的。

其他

因为不需要整块的背光层，因此OLED设备具有薄、可折叠、续航好的优点

当然也存在一些缺点，比如寿命短（因为OLED电压直接作用于二极管发光体，而LCD针对的是液晶层），容易烧屏、伤眼。

未来的显示技术

目前还有处于试验状态未量产的MicroLED、以及与其同源的MiniLED，都是LCD以及OLED的改进。这里不过多赘述，有兴趣可以自己了解下。

光栅化

三角形是图形学的基础

三角形 Triangle 的优点

• 最基本的多边形
• 其他的多边形都可以拆解成三角形
• 三角形内部一定是处在一个平面

现在我们的目标是如何将二维平面上三角形与像素的映射关系对应，即我们想要把连续的图形转化为离散的点

采样 Sampling

采样 Sampling：将一个函数离散化的过程。从连续信号中按照一定的时间间隔或空间间隔提取离散数据点的过程。可以用以下代码来理解采样做了什么事

for (int x = 0; x < max; ++x)
	output[x] = f(x);

因此，对于一个指定的二维平面中的三角形，我们需要做什么？我们需要的是判断屏幕上的所有点是否属于三角形内。

我们可以定义以下函数

$$F_{inside}(t,x,y)=\{\begin{array}{l}1\text{point(x, y) in triangle t}\\ 0otherwise\end{array}$$

即简单来说，我们就想做这样的事：

for (int x = 0; x < width; ++x)
    for (int y = 0; y < height; ++y)
        output[x][y] = F_inside(tri, x + 0.5, y + 0.5);

因此，如何实现F_inside这个方法呢？也就是如何判断一个点是否在三角形内？

回忆线性代数的知识，可以用向量的叉乘来进行

$$\mathbf{a}\times \mathbf{b}=||\mathbf{a}|||\mathbf{b}||\sin \theta =\mathbf{a}\times \mathbf{b}=\left|\begin{array}{ccc}\mathbf{i}& \mathbf{j}& \mathbf{k}\\ a_1& a_2& a_3\\ b_1& b_2& b_3\end{array}\right|$$

因此通过判断结果的正负来确定其向量的夹角，进而判断点是否在三角形内部

判断准则

• 若三个叉积的 z 分量符号相同（全为正或全为负），则点 P 在三角形内。
• 否则，P 在三角形外

可以自行从几何的角度想一下～需要注意，向量的构造顺序要一致，比如有ABC三个顶点，则构造时为 AB与AP BC与BP CA与CP。

这里暂时不考虑点落在三角形边上的情况

对每个像素点都进行如上函数的判断，我们就有了0 和 1的映射结果，假设上色的颜色是一致的，我们就有了以下图形。看起来是不是有点像了。

Rasterization-Example-1

Rasterization-Example-2

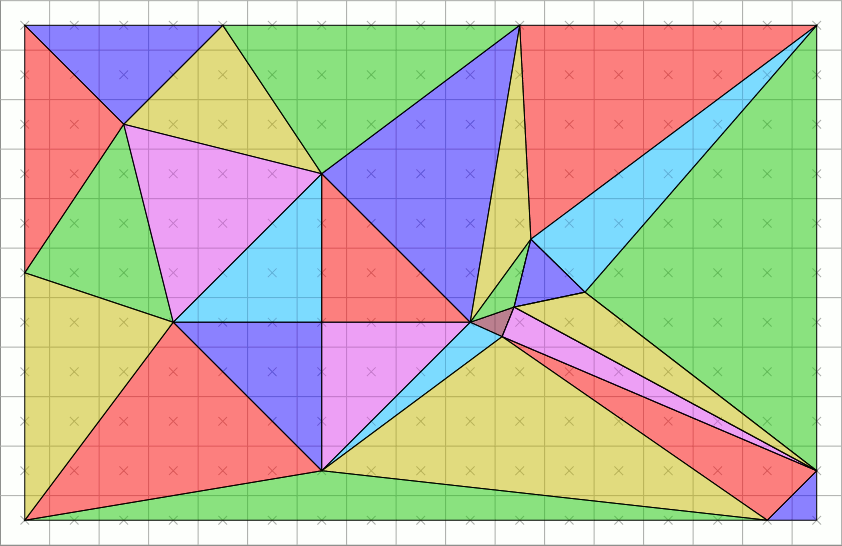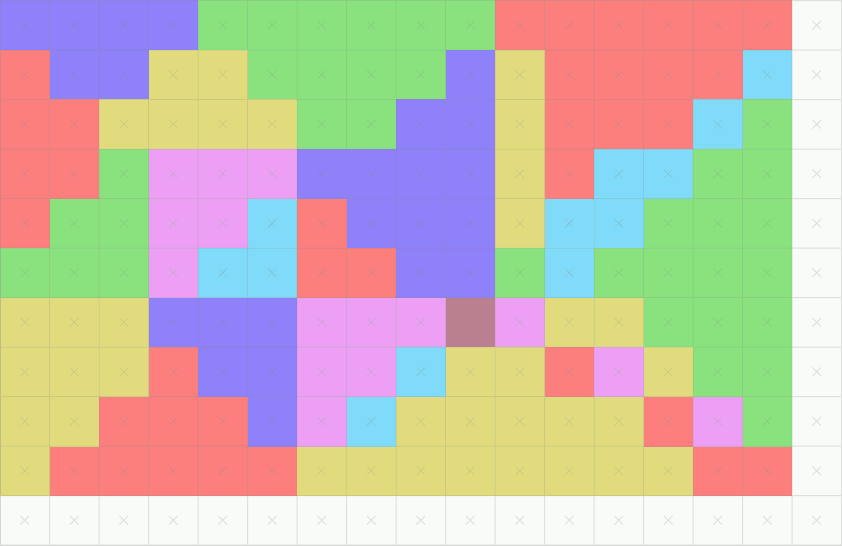
但也需要注意的是，在分辨率较低的情况下，似乎上图看起来不是那么像，存在一些锯齿？没有看起来那么丝滑？因为我们想要的是三角形，但实际得到的只是一个锯齿状的图形(Jaggies)，产生了信号走样(Aliasing)的问题。因此，我们想要图形真实，那就需要抗锯齿。

Anti-Aliasing 抗锯齿 / 反走样

定义

抗锯齿是一种消除显示器输出的画面中图物边缘出现凹凸锯齿的技术，那些凹凸的锯齿通常因为高清晰度的信号以低分辨率表示或无法准确运算出3D图形坐标定位时所导致的图形混叠（aliasing）而产生的

为什么采样会出现走样情况？（个人理解）

因为受像素点个数和形状的影响，会存在一些情况，需要最小像素点表现为三角形或多边形时，其仍然只能表现为正方形选中或不选中，因此原始数据受到了改变。

对于采样时产生的误差，通常称为Sampling Artifacts

采样还会产生摩尔纹，比如拿手机拍显示器屏幕，以及产生车轮效应

出现误差的本质：信号变化太快，采样太慢。

具体措施

先模糊处理再采样

那这样将一张图片模糊化呢？这就涉及到图像处理的技术

在图形学中窥探数学

这里由于涉及到图像处理相关的技术，因此需要涉及的知识较广，甚至可以单独成册，这里自己就不再写出原理，只给出相关知识点，可以再回顾一下

• 采样的意义，为什么要采样？

• 采样过低会造成什么问题？香农定律

• 时域与频域的概念

• 傅立叶变换的基础、意义及原理

• 高频控制细节，低频控制轮廓？

• 投影，如何计算一个向量在另一个向量的投影？

• 复平面的意义？i与e的定义，欧拉公式的几何意义

• 三角函数的正交性以及希尔伯特空间

• 傅立叶变换绘图与正弦函数叠加的几何意义

• 采样点的疏密程度以及傅立叶级数中确定的级数对变换的函数与原始数据的贴合成都的影响

• 为什么傅立叶变换既可以来处理波形图又可以来进行绘图？（从不同的角度看圆周运动）

滤波：把某个特定频率的内容、信号、数据抹掉

高通滤波与低通滤波对图像的影响

滤波、求平均与卷积

从频域看走样

MSAA：目的：模糊。细分单个像素，根据单个像素内细分的子像素处于三角形内的占比来判断色值比例

FXAA Fast Approximate AA

TAA Temporal AA

Z-Buffer 深度测试

目的：决定哪些像素可见（前面的物体遮挡住后面的物体）

传统的绘画观念(Painer’s Algorithm)：从远往近画，近层覆盖远层。但需要先排好序($O(N\log N)$时间复杂度)。❗ 但在计算机图形学中，特定图片下会存在问题。

因此图形学引入了一个概念：Z-Buffer (深度缓存)

这里认为深度缓存的值越小，说明物体离视点越近，反之越远。

核心措施

深度缓存发生在每一个像素内。给予每一个像素点深度缓存的值，光栅化每一面时，除了有一个最终渲染的画面，还会构建一个带有深度缓存值的画面，来计算像素点是否在面内，若在面内，则会有条件地替换掉该像素的色值与深度缓存值。

for (each triangle T)
    for (each sample(x, y, z) in T)
        if (z < zbufferf[x, y])
            framebuffer[x, y] = rgb;
			zbuffer[x, y] = z;
		else
            ;

undefined

时间复杂度: $O(N)\text{(for }\mathit{\text{N}}\text{ triangles)}$ ，且物体远近与与绘画顺序无关了。

深度值完全一样该怎么处理？ 这里暂时还不知道～

Shading 着色

图形学中着色的定义：对不同物体应用不同材质，包括光照、明暗

Blinn-Phong Reflection Model

undefined

一个较简单、基于经验的光照模型(并不完全符合物理)，在Phong反射模型中，光照有三部分组成：

$$I=I_a+I_d+I_s$$

• Specular hightlights 镜面反射光
• Diffuse reflection 漫反射
• Ambient lighting 间接光照

undefined

Shading Point：上色点，认为是一个平面(可能是非常小，但也归纳到平面范畴)

Shading is Local 着色的局部性质

不考虑其他因素，不考虑其他任何点的存在。只考虑光照的方向以及该点的光照，

Light Fallout 光衰弱

光衰弱是指光的强度随着距离的增加而逐渐减弱的现象，符合物理世界中逆平方定律(Inverse Square Law)，光源发出的光在远离光源的过程中能量分布变得稀疏

直觉上：站在手电筒附近，会觉得很亮，但站的很远，则觉得没那么亮（但个人感觉是否跟空气中的微粒吸收了部分光有关？）

与光在空间中扩散的物理特性有关，光线在更远的距离上覆盖更大的区域，导致单位面积上光的能量减少。

点光源发出的光遵循逆平方定律：

$$I=\frac{I_0}{d^2}$$

推导

推导也比较简单，以3D视角看点光源发出的光，光源发出的光能量均匀分布在球面上。而球的表面积计算公式为$S=4\pi r^2$，而由于总能量不变(光速恒定)，因此单位面积上光能量随着离光源距离的平方的增加而减少。

undefined

Diffuse Reflection 漫反射

某一点接收到的光照会反射到所有方向。

Wiki: 漫反射（Diffuse Reflection）是光照在粗糙表面上发生的非定向反射（但每个微小表面仍然遵循镜面反射定律（入射角=反射角），由于这些微小面取向各异，导致光线朝多个方向反射），使得物体看起来具有均匀的亮度。

朗伯特表面（理想的漫反射表面），朗伯特余弦定律$I=I_0\cdot \cos \theta$ 反射光强度等于入射光强度乘其夹角的余弦值。当然现实世界中没有完全的朗伯特表面

undefined

如何理解漫反射

1. 为什么会有冬天和夏天？根据太阳光射向某一点的角度，即光照方向与该平面的法线所成的夹角，夹角越小越热，夏天时即夹角较小。
2. 为什么白纸在任何角度看起来都亮？纸张表面有无数微小的凸起，导致光线以不同方向反射，形成均匀的漫反射。
3. 为什么金属不像塑料那样漫反射？金属表面更光滑，反射更多的镜面反射，所以亮度依赖于观察角度。

如何理解朗伯特余弦定律？

一矩形光柱，光通量为 $\mathrm{\Phi }$ 的光，垂直地打在一个平面上，光照区域为光柱横截面积$A$。随后倾斜这个平面，此时光照区域为$\frac{A}{\cos \theta }$, 其中 $\theta$ 为光柱与平面法线的夹角。可以自己画图理解下。此时单位面积的光照强度就为 $\frac{\mathrm{\Phi }}{\frac{A}{\cos \theta }}$

因此，有漫反射能量公式:

$$L_d=k_d(\frac{I}{r^2})max(0,\widehat{\mathbf{\text{n}}}\cdot \widehat{\mathbf{\text{l}}})$$

其中

• $k_d$ 为反射处材质对光的不吸收率，可以转化为三通道的$(R,G,B)$的向量分量
• $\widehat{\mathbf{\text{l}}}$ 为指向光源的单位向量

Specular Term 高光

观察视角与光源的反射线近乎一致时，认为会产生高光效果

定义半程向量 half vector 的概念，如下图中的 H

$$\begin{array}{rl}\mathbf{\text{h}}& =bisector(\mathbf{\text{v}},\mathbf{\text{l}})\\ & =\frac{\mathbf{\text{v}}+\mathbf{\text{l}}}{||\mathbf{\text{v}}+\mathbf{\text{v}}||}\end{array}$$

undefined

再通过与法向量的点积来确定来者的夹角。

但实际上高光的效果是角度非常小的时候才会出现高光效果，而cos的效果在角度较大时也会产生高光，因此这里用了一个比较巧的办法，通过cos的n次方不断地弱化大角度下高光并增强小角度下高光效果。

如下表示在cos不同的次方下，图像的变化

image-20250220105440062

因此有高光的反射能量计算方程

$$L_s=k_s(\frac{I}{r^2})max(0,\widehat{\mathbf{\text{n}}}\cdot \widehat{\mathbf{\text{h}}}{)}^p$$

Ambient Term 环境光

实际上除了光源的光，还有环境中不同的光（来自四面八方）照射到此点进行反射。环境光非常复杂

$$L_a=k_a{I}_a$$

这里，我们只是做了简化，将 $k_a$ 当作一个常数，计算出一个模糊的环境光，但实际上的运算还需要用到全局光照的因素

因此现在我们对上述过程有了更清晰的认知

undefined

Shading Frequencies 着色频率

看一下常规的上色流程：

• 先基于面进行上色
• 基于每个顶点进行上色并
• 基于每个像素进行上色

img

img

img

Flat Shading 平直着色法

基于“组成模型的多边形都是平的”的假设，认为同一多边形上任意点的法线都相同

先在每个多边形上挑选一个点计算颜色（通常是多边形的第一个顶点，如果是三角形网格则也可以选择几何中心），则该多边形上其余点都直接使用该点的颜色。所以，使用平直着色法的每个多边形上都是统一的颜色。

这样绘制出来的每个三角形内颜色都是统一的

img

Gouraud Shading

基于每个顶点的法线，单独求出每个顶点的颜色，三角形内部颜色基于插值来计算，因此有了颜色的过渡。为多边形表面生成连续的明暗变化

Gouraud着色的球体，注意高光处的表现

Phong Shading

结合了多边形物体表面反射光的亮度，并以特定位置的表面法线作为像素参考值，以插值方式来估计其他位置像素的色值。

Phong着色法的效果更逼真，能够提供更好的光滑曲面的近似值

Flat Shading vs Phong Shading

计算顶点的法线

以上Gouraud Shading以及Phong Shading都用了 顶点的法线的概念，那在实际中，如何求一个顶点或任意位置的像素的法线呢？

正常思维下，我们可能这样计算，即找出这个点所在平面，并基于该点做出与这个平面相切的平面，求得的该平面的法向量即为该点的法向量。

img

如何求得像素点的法向量

法线应该是连续变化的，因此可以通过某种插值方法来计算。

Pipeline 管线

管线：代表一系列不同的操作

GPU即实现了一系列的管线

graphics pipeline

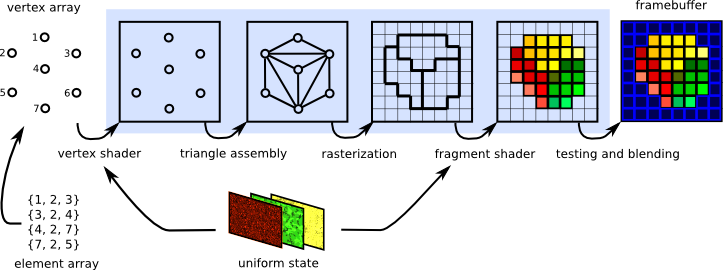
Shader 着色器

着色器是可编程的

Shader Program是可被显卡识别并执行的语言

Barycentric Coordinates 重心坐标

引入重心(质量中心)的目的：方便进行三角形内部的插值计算，进行平滑的过渡

对任意一个三角形ABC, 对其内的一点P，有

$$\begin{gathered} P={\lambda }_{1}A+{\lambda }_{2}B+{\lambda }_{3}C \\ {\displaystyle 1={\lambda }_1+{\lambda }_2+{\lambda }_3.}({\lambda }_1>0{\lambda }_2>0{\lambda }_3>0) \end{gathered}$$

且有

$${\lambda }_1=\frac{{\mathrm{△}}_{PBC}}{{\mathrm{△}}_{ABC}}$$

${\lambda }_2{\lambda }_3$ 类似

而三角形自身重心为

$$G=(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3})$$

在重心坐标下，重心的表示为：

$$G=(\frac{1}{3},\frac{1}{3},\frac{1}{3})$$

Texture Mapping

任何一个三维物体的表面都是2维的

纹理是什么？

纹理就是一张图

纹理映射：纹理通过拉伸或缩放，来贴附在一个三维物体的表面

undefined

纹理坐标系 U-V

Applying Texture

Magnification

分辨率与纹理大小的问题，如果纹理太小了怎么办？插值

几种不同的插值方式(Interpolation)

undefined

Nearest-neighbor 最邻近插值 最简单，寻找最近的纹理像素

Bilinear 双线性插值。基于周围的四个点，在x、y方向上分别进行插值计算

优点：变换更平滑

$$\begin{gathered} {\displaystyle \begin{array}{rl}f(x,y_1)& \approx \frac{x_2-x}{x_2-x_1}f(Q_{11})+\frac{x-x_1}{x_2-x_1}f(Q_{21}),\\ f(x,y_2)& \approx \frac{x_2-x}{x_2-x_1}f(Q_{12})+\frac{x-x_1}{x_2-x_1}f(Q_{22}).\end{array}} \\ {\displaystyle \begin{array}{rl}f(x,y)& \approx \frac{y_2-y}{y_2-y_1}f(x,y_1)+\frac{y-y_1}{y_2-y_1}f(x,y_2)\end{array}} \end{gathered}$$

undefined

Bicubic 双三次插值，是双线性插值的扩展版本，使用 三次多项式（Cubic Polynomial） 来进行插值计算，在 X 和 Y 方向上各自使用三次多项式插值。取周围16个采样点的的加权平均得到

优点：更丝滑，锯齿感更小

缺点：计算量大

Minification

纹理小了引发的问题

如果纹理大了怎么办？问题可能更严重，因为从逻辑上来讲，如果是纹理小了，在magnification时，如果采用双线性插值Bilinear，我们并没有丢失掉原有数据，反而是新增了数据，这很大程度上不影响一个物体的特性。但如果是纹理大了，那在缩小时，我们必须要删除这个物体的部分信息，因此其物体特征可能就会消失。产生走样问题。具体表现为：远处产生摩尔纹，近处产生锯齿

解决方案

1. SSAA, SuperSampling AntiAliasing 超采样, 一个像素用多个采样点。计算成本高
2. Mipmap

Mipmap

Mipmap（多级渐远纹理） 是一种 纹理映射优化技术，来处理远距离下纹理的采样问题（大纹理对应小画布）。为了加快渲染速度和减少图像锯齿，贴图被处理成由一系列被预先计算和优化过的图片组成的文件,这样的贴图被称为 MIP map 或者 mipmap

目的：在远距离/大纹理小画布场景下减少混叠（Aliasing），提高渲染效率

只能做近似地、矩形地查询

Image showing how mipmaps reduce aliasing at large distances.

以原图层为Level0，每层以上一层进行分辨率缩放

Mipmap levels

缺点是Mipmap会引入额外的空间占用，造成近乎额外1/3的存储，如下图所示

img

如何应用Mipmap？

基于屏幕像素，计算映射到纹理空间后对应的纹理的近似矩形空间大小

根据该矩形空间的大小，来在对应的nxn的mipmap上查询，例如：

• 矩形空间大小为4 x 4，则在Level-2查询该像素
• 矩形空间为1 x 1，则在Level-0查询该像素

但如果矩形空间存在小数或为3 x 3呢？此时会出现锯齿效果（因为突变）

则一样基于插值解决突变效果，用双线性插值在邻近的图层进行计算，被称为 三线性插值(Trilinear Interpolation。让同一个物体不同远近有了更平滑的变化。

undefined

缺陷

使用Mipmap时，若距离较远时，则会产生非常模糊的现象 Overblur

这是因为：Mipmap只能查询矩形的均值且基于插值，采用的是近似的求值。且Mipmap是长宽同时变化，而不是只针对长或宽进行变化

可以使用各向异性过滤来解决

undefined

Anisotropic filtering 各向异性过滤

各向异性：在不同的方向上表现各不相同

屏幕的像素映射到纹理上时，不一定都是矩形（长宽相等），很有可能映射为长条形状的四边形体现为横向或纵向的拉伸或压缩

但本质上还是没有解决问题，对于一些特殊映射，比如一个像素被映射为倾斜的四边形，此时各向异性过滤也不能很好地处理

缺点：空间总开销变为原来的三倍

undefined

各向异性的层数

游戏设置里，各向异性一般会让玩家设置层数，比如2x 3x，就是图像压缩的层数，最终是收敛到该图像的三倍。因此，显存足够的情况下，各向异性开到最高即可～

其他的过滤方式

EWA Filtering: 原理，基于圆形来覆盖

Environment Light Mapping 环境光映射

不同的方式来记录不同方向的光照信息：

1. Spherical Environment Map

用球的表面 (2D) 来记录来自任何位置的光。采用 预先渲染的球面反射图像（称为球面贴图），并将其 投影到 3D 物体表面，模拟 环境反射。

illustration of a sphere map of the inside of a building

会存在扭曲问题

2. Cubic Map

将载有环境光的球体用正方体包裹，并映射到其6个表面，则有了完整的环境光

undefined

undefined

贴图技术

Bump Mapping 凹凸贴图

每个待渲染的像素在计算照明之前都要加上一个从高度图中找到的扰动。这样得到的结果表面表现更加丰富、细致，更加接近物体在自然界本身的模样。

基于法线变化实现凹凸贴图 ，凹凸贴图在边缘会露馅，因为未改变物体几何

undefined

把高度图（Height map）转换成一张法线图（Normal Map），其图的RGB分别是原高度图该点的法线指向：Nx、Ny、Nz。最后在渲染的时候直接将该高度图的每个像素与光源的向量点乘，即可得到表示每一点的明暗系数的图

Displacement Mapping 位移贴图

Cartesian transport

Other Applications

• 3D纹理

Geometry 几何

几何的表示

**如何来描述一个特定形状的物体？**如何在计算机图形中来描述一个物体的几何形状？

隐式地表示几何 Implicit

一系列满足特定关系的顶点 (eg. $x^2+y^2+z^2=1$)

$$f(x,y,z)=0$$

一般地，很难从表达式来看出几何形状

但很容易能判断一个点是否在该形状内外

Algebraic Surfaces (Implicit)

x y z的数学公式表达

缺点：不直观

Constructive Solid Geometry

undefined

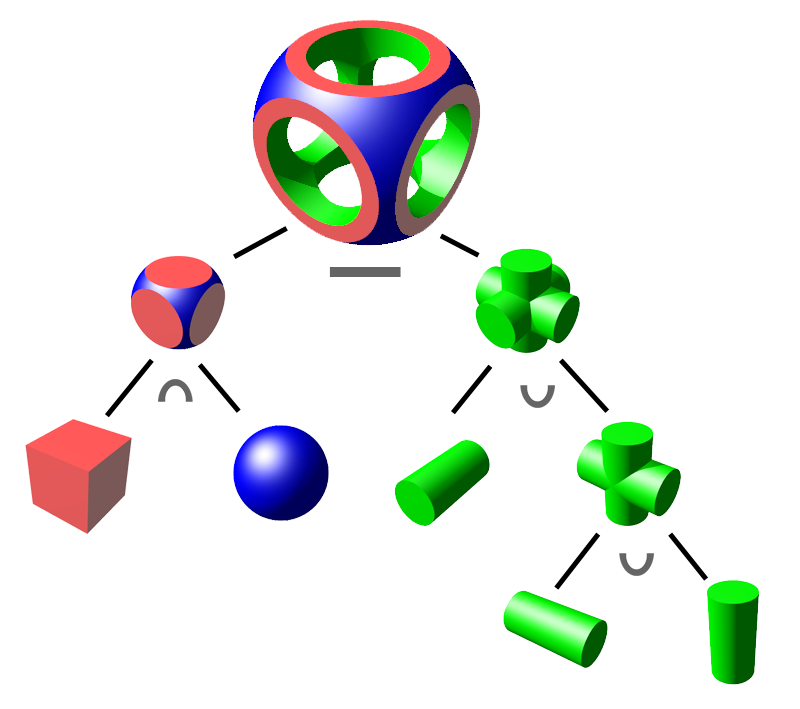
定义几何之间的布尔运算关系，能够进行几何结合

(Signed) Distance Functions 距离函数

Distance Function 是一个函数 d(p) ，它返回 点 p 到某个几何对象的最短距离。

对于一个几何对象 O ，距离函数 d(p) 定义为：

$$d(p)=\text{min}(\parallel p-x\parallel ),x\in O$$

• p 是任意点
• x 是 对象 O 上的一个点
• d(p) 返回 p 到 O 的最短欧几里得距离

Signed Distance Function（SDF） 是一种特殊的距离函数，它不仅提供 点到表面的距离，还提供 点相对于表面的方向信息（内部/外部）

应用：碰撞检测

$$SDF(p)=\{\begin{array}{ll}\text{正数（> 0）},& p\text{ 在物体外部}\\ 0,& p\text{ 在物体表面}\\ \text{负数（< 0）},& p\text{ 在物体内部}\end{array}$$

Level Set Method 水平集方法

与距离函数类似，类似于等高线

undefined

Factals 分形

一个粗糙或零碎的几何形状，可以分成数个部分，且每一部分都（至少近似地）是整体缩小后的形状”

undefined

显示地表示几何 Explicit

要么直接给出，要么通过参数映射(parameter mapping)，类似参数方程的方式，的给出

$$f(u,v)=g(u,v)$$

容易看出形状

难以判断一个点是否在形状内外

更高级地，如何来表示两个几何形状的不同程度地结合？这有多种方法来应对

Point Cloud 点云

只要点足够多，就能近似地表示一个物体

点云的密度大

undefined

Polygon Mesh 多边形网格

将物体拆分为多个简单的凸边形表示

图形学中最广泛的显示表示几何的方法

undefined

Wavefront .obj Object

由WaveFront科技公司开发，图形学中来表示一个物体的文件，包括物体的顶点、法线、纹理坐标

# List of geometric vertices, with (x, y, z, [w]) coordinates, w is optional and defaults to 1.0.
v 0.123 0.234 0.345 1.0
v ...
...
# List of texture coordinates, in (u, [v, w]) coordinates, these will vary between 0 and 1. v, w are optional and default to 0.
vt 0.500 1 [0]
vt ...
...
# List of vertex normals in (x,y,z) form; normals might not be unit vectors.
vn 0.707 0.000 0.707
vn ...
...
# Parameter space vertices in (u, [v, w]) form; free form geometry statement (see below)
vp 0.310000 3.210000 2.100000
vp ...
...
# f v1 v2 v3
# f v1/vt1 v2/vt2 v3/vt3
# f v1/vt1/vn1 v2/vt2/vn2 v3/vt3/vn3
# Polygonal face element (see below)
f 1 2 3
f 3/1 4/2 5/3
f 6/4/1 3/5/3 7/6/5
f 7//1 8//2 9//3
f ...
...
# Line element (see below)
l 5 8 1 2 4 9

Bézier curve 贝塞尔曲线

核心： 描述曲线

给出多个顶点，不一定经过中间点，最终形成从起点到终点的一条曲线

undefined

Quadratic Curves

给出三个点，来画一个二次的贝塞尔曲线，二次的贝塞尔曲线存在三个控制点 P0 P1 P2, 其中P0 P2分别为起点与终点

$$\frac{P_0{Q}_0}{P_0{P}_1}=\frac{P_1{Q}_1}{P_1{P}_2}=\frac{Q_{0}B}{B_{Q}1}=t=0.25$$

Construction of a quadratic Bézier curve

随着t不断增大，B点的位置变化便构成了一条曲线。

Animation of a quadratic Bézier curve, t in [0,1]

更高维度的

Animation of a quartic Bézier curve, t in [0,1]

Formula 公式推导

几何意义我们已经知道，那在数学公式上该如何表示呢？如何用t进行表示最终落点位置呢

几何流程上，我们是顺序地进行线性插值并计算出最后的结果

这里不再列出推导流程，理解即可。

$${\displaystyle \mathbf{B}(t)=\sum _{j=0}^n{t}^j{\mathbf{C}}_j}$$

n代表有几个控制点

重要性质

1. 对所有控制点做仿射变换 与 对曲线做仿射变换 的效果是一样的。

2. 画出的曲线的控制点都需要在图形的凸包内（基于切线或者导数来理解）。 画出的贝塞尔曲线的点，一定在这个凸包以内

   

   undefined

Piecewise 逐段贝塞尔曲线

如何精细地控制一个曲线？很多时候我们不像牵一发而引全身。因为动一个控制点，则整条曲线都会发生变动

一般地，定义每4个控制点来确定一条贝塞尔曲线。以此顺序地、连续地确定一整条曲线，这样每次改变一个点时，只会影响其相邻的子曲线。

自己来试一下逐段贝塞尔曲线的控制：Bezier Curve Demos

是不是与Photoshop上曲线绘制很像？

连续性

C0连续：两端贝塞尔曲线，一段的结尾是另一段的起点

C1连续：两段贝塞尔曲线，除在C0连续基础上，其导数也连续

C2连续：除在C1连续基础上，其二阶导数也连续

...

Splines 样条

B-Splines

极其复杂，对贝塞尔曲线的扩展

可能是图形学最难的几何表示方式

曲线表示平面

如何以多条曲线来表示一个平面？

以不同的曲线，基于同一参数t，获得一条新的贝塞尔曲线，再以此为控制点，该条曲线在不断扫过空间的时候，就形成了一个曲面。

例子: Making MathBox

Mesh Operations 网格操作

图形学中，物体是由面构成的，构成一个个的网格，对于这些网格，有多种操作方式

Mesh Subdivision 网格细分

目的：增加细节，增大分辨率 Increase Resolution

img

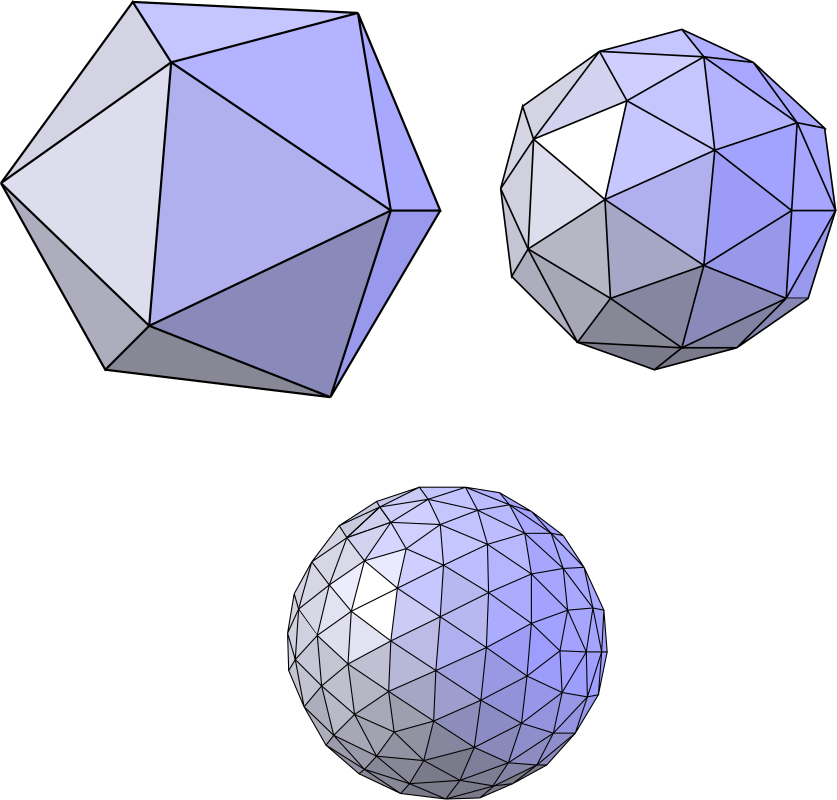
Loop Subdivision

Loop是人名......

将一个三角形分为四个小三角形（以某一种特定方式），并进行位置调整

总的来说做了两件事：细分 + 调整

img

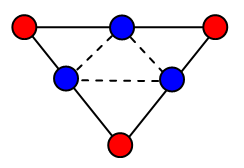
如何细分？

按照如下加权方式计算

计算新产生的顶点

img

$$\frac{3}{8}\ast (A+B)+\frac{1}{8}\ast (C+D)$$

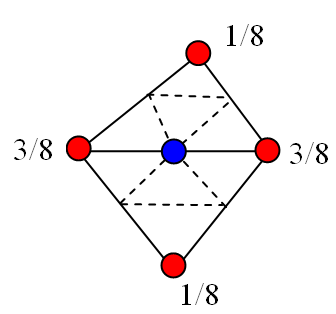
其中A、B是与中间点共边的点，C、D是不共边的点

如何调整？

调整，即更新老的顶点

img

$$\begin{gathered} P_{new}=(1-nu)\ast P_{old}+u\ast \sum neighbors \\ n=\text{vertex degree} \\ u=\{\begin{array}{l}\frac{3}{16},n=3\\ \frac{3}{8n},n>3\end{array} \end{gathered}$$

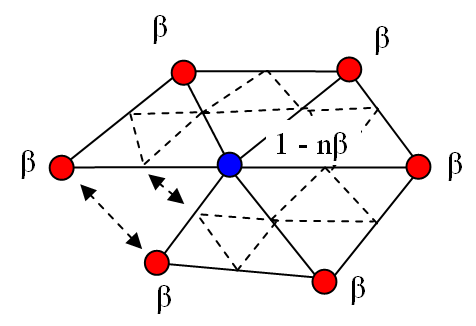
Catmull-Clark Subdivision

更广为人知的细分方法

Loop细分只针对三角形网格，对于四边形网格则不适用，而该细分方法能适用于多边形网格

奇异点 Extraordinary Vertex: degree != 4

步骤一样为 细分 + 更新

这里不细究了

Mesh Simplification 网格简化

目的：简化物体，尽量保持物体形状，提高性能

不同场景下， 用不同层级的几何模型

img

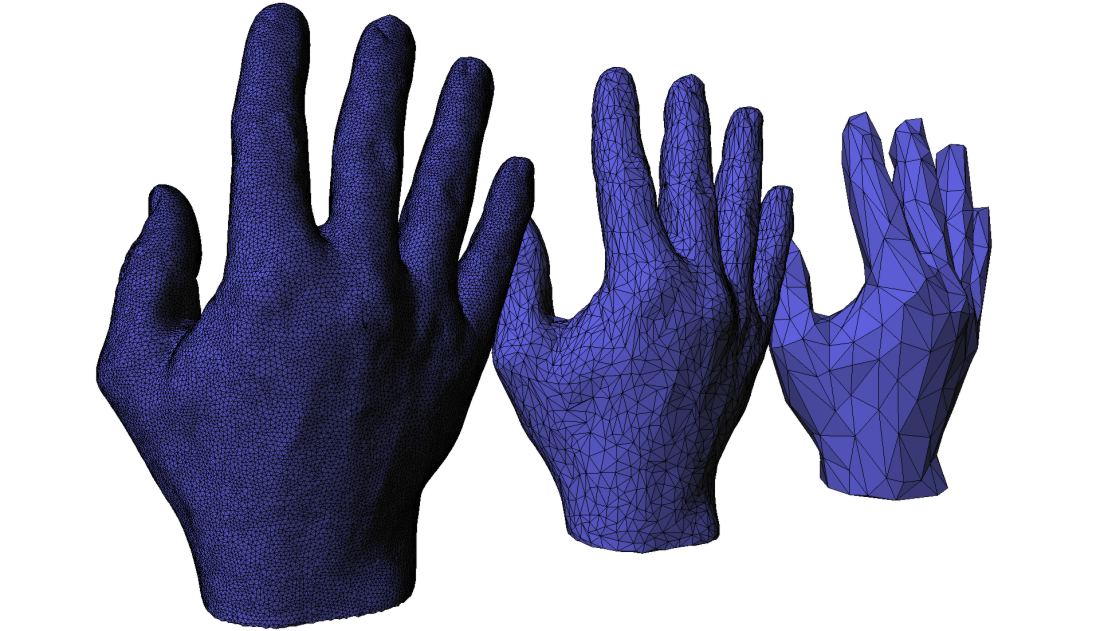
Edge Collapse

ECOL VSPLIT

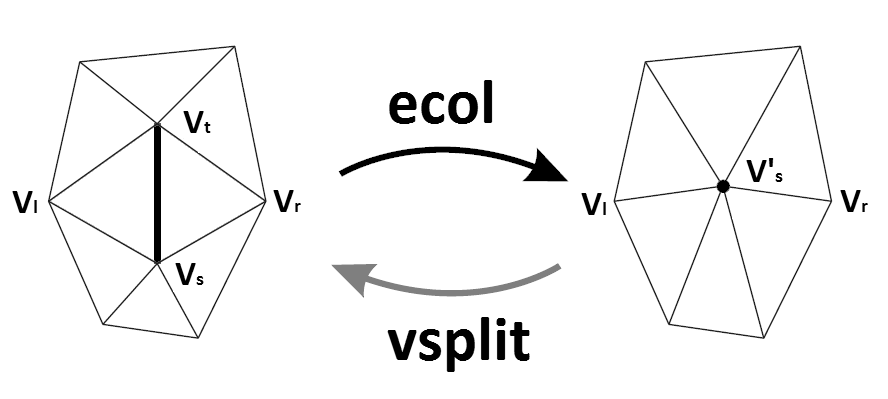
二次度量误差 Quadrtic Error

选二次度量误差最小的那几条边进行坍缩，注意一条边坍缩后，周围的边都可能受影响，要重新计算。

Mesh Regularization 网格

目的：提升图片质量

Ray Tracing 光线追踪

游戏中是如何显示阴影的？光线打在人物上，在地面上映出的影子

undefined

如何用光栅化画出阴影？

阴影映射方法：Shadow Mapping

Shadow Mapping

核心：投影+深度测试+两次渲染

点不在阴影里的定义：Camera能看到这个点且(从光的角度)光也能看到这个点

点在阴影里的定义： Camera能看到这个点但光看不到这个点

阴影会产生走样

点光源下如何生成阴影？

1. 认为光源为一个虚拟相机并设置一个虚拟平面用于投影
2. 从光源看向场景，记录能看到顶点的深度
3. 摄像机看顶点，（通过投影）对比深度

这个过程中也会因为虚拟平面（阴影图）的大小而产生误差(投影、浮点数的影响)

先从光源往场景看，得出深度，再从实际观测点出发，对比。开销更大，因为需要渲染整个场景两遍，并且渲染的是硬阴影（阴影边界清晰锐利，光照区域和阴影区域之间存在明显的分界线，不自然）

硬阴影 vs 软阴影

硬阴影：阴影边界清晰锐利，光照区域和阴影区域之间存在明显的分界线。计算较简单，主要基于几何投影（Shadow Mapping 或 Shadow Volumes）。由点光源产生。

软阴影：阴影边界模糊、平滑过渡，即在光照区域和完全阴影之间存在半影区（Penumbra）。由面光源（Area Light）或体积光源（Volumetric Light） 产生，因为光线来自多个方向，不同角度的光线可能部分遮挡或完全遮挡。软阴影更加真实

img

用日食的现象来看软阴影

Illustration image

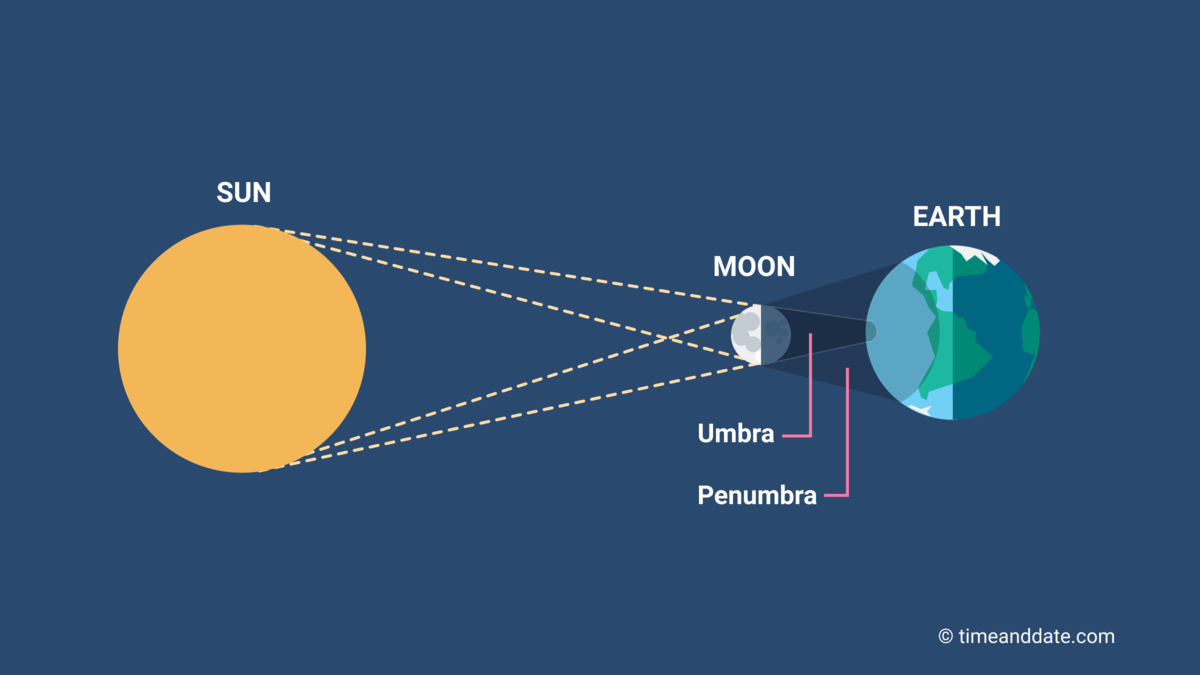
本影 Umbra：阴影的黑暗核心站在本影内，您将无法看到光源的任何部分

半影 Penumbra: 阴影较亮的外部

比如在下半部分的半影区，则只能看到下半部分的太阳，而看不到上半部分（因为来自上半部分的光都被月球遮住了）

基础

为什么会引入光线追踪

光栅化的问题是无法表达一些全局的效果，包括在处理软阴影Soft Shadow、高光反射 Glossy Reflection、间接光照 Indirect Illumination等效果

光栅化 vs 光线追踪

并且光栅化是一种很快、很近似的渲染方式，针对地实时的应用

光线追踪是一种准确地但非常慢的渲染方式，一般针对离线的应用 Offline(电影)，一帧需要花费10K CPU小时

光线的定义 Light Rays

• 沿直线传播(现实空间中这是错误的)
• 光线间不会发生碰撞(现实空间中是错误的)
• 光线从光源出发到观测者眼睛
• 光线是射线

光具有可逆性 赋予了 光线追踪 的可行性, 从观察者视角出发而不是光源本身

光线被定义为方向向量 + 光源点

Whitted-Style Ray Tracing

递归的射线追踪

当不同物体的光都进入观测投射平面的同一位置时，此时便会基于不同物体反射光(带有能量衰减)的加权来进行计算该像素的色值

Follow up rays for effects

因此将光线分为：

• primary ray: 从人眼发出的光
• secondary ray：经过反射、折射后一系列的光

细节

光线方程 Ray Equation

$$\mathbf{\text{r}}(t)=\mathbf{\text{o}}+t\mathbf{\text{d}}$$

其中

• t -> time
• o -> origin
• d -> direction

如何求光线与各种二维、三维物体(比如圆)的交点？ 高中数学，这里不赘述

光线与平面(三角形)求交

平面方程 Plane Equation

给一个平面上的一个点p’ 以及 该平面的法线N，对于平面上任何一个点P，有

$$(p-p^{\prime })\cdot N=0$$

最终满足平面方程

$$ax+by+cz+d=0$$

常规方法求三角形与射线的交点：

1. 求平面与射线的交点
2. 判断该点是否在三角形内

Möller–Trumbore intersection algorithm

快速求射线与三角形的交点，基于三角形某一点都可以用重心坐标这一原理来表示

$$O+tD=(1-b_1-b_2)P_0+b_1{P}_1+b_2{P}_2$$

但平面与射线求交点，原始做法非常慢（考虑所有三角形，每个像素打出一根光线（包括光线反射折射），与所有三角形求交点），这个工作量是非常巨大的

包围盒 Bounding Volumes

将一个物体用一个简单几何体包围起来，如果光线连这个几何体都触碰不到，则更不用说碰到里面的物体了。

undefined

首先要理解 一个box(长方体)是三对对立面平面(slabs)的交集

我们经常使用轴对齐包围盒 Axis-Aligned Bounding Box (AABB) （简化了计算）

如何基于包围盒来判断光线是否进入该盒子

光线进入盒子 = 光线进入三个对立面

对于三个不同的对立面，与一条光线，有

1. 射线穿过一对对立面时存在两个交点，$t_{min}$ 与 $t_{max}$
2. 在$t_{min}$ 与 $t_{max}$之间，该点位于该对立面内
3. 对于三对平面，对于给定时间t，当且仅当t均在每个对立面的$t_{min}$ 与 $t_{max}$之间时，该点位于这个包围盒内(make sense)
4. 因此：光线进入该包围盒时间 $t_{enter}=max(t_{min})$ 光线离开该包围盒时间 $t_{exit}=min(t_{max})$ (make sense)
5. 如果$t_{exit}<0$ 则说明盒子与光线无交点
6. 当且仅当 $t_{enter}<t_{exit}\mathrm{\&}\mathrm{\&}t\ge 0$ 时该光线与该包围盒有交点

如何进行加速计算

Acceleration Grid加速网格

步骤1. 构建加速网格 Acceleration Grid

image-20250302160844369

步骤2. 光线与平面求交

image-20250302160919310

需要注意的是，光线与盒子有焦点，不意味着光线与盒子的物体有焦点。

但这个方法在有大规模的集中物体的情况便不使用

Spatial Partitions 空间划分

Oct Tree 八叉树

undefined

K-D Tree

undefined

BSP Tree

这里主要介绍KDTree

KD Tree的划分过程如下

用KDTree如何判断光线与平面中的物体有交点？

注意：叶子节点中，需将所有物体与该光线求交

但这样存在一个性能问题，如果一个物体同时占据3、4、5区域，且光线经过了3、4、5这一个大区域，那则在3、4、5内都需要判断光线与物体是否有交点，似乎有点性能浪费，因此我们有了

Bounding Volume Hierarchy BVH

应用非常广泛，主流的方法

划分的不是空间，而是物体，因此最终为物体仅出现在一个包围盒里。

undefined

但BVH划分后的包围盒之间可能相交

img

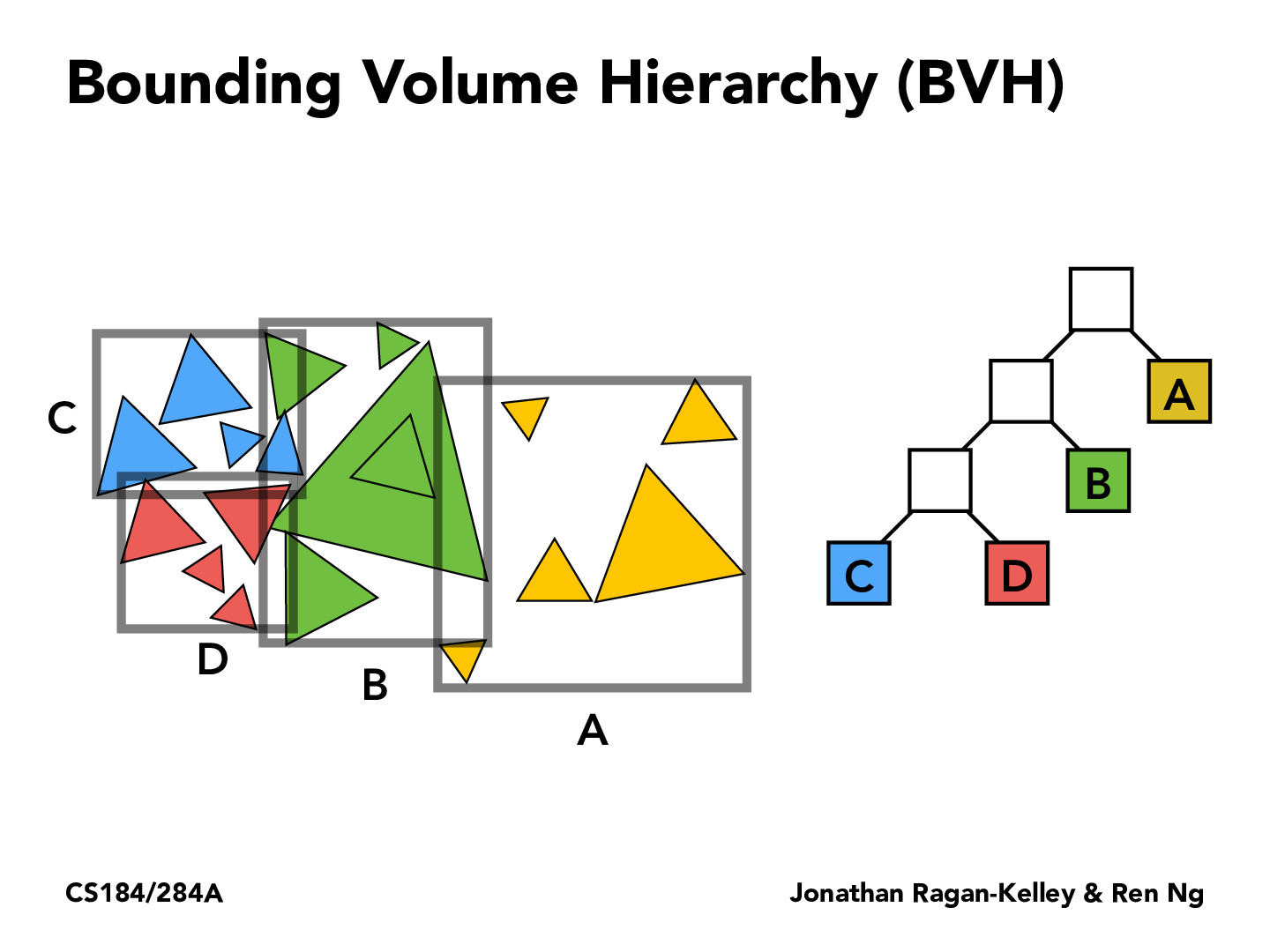
因此如何划分包围盒则非常重要

希望划分的尽量均匀(每个包围盒内节点数量相近或包围盒大小类似，不同的划分方式)

• 选最长的坐标轴划分(空间中盒大小尽量均匀 )
• 选中间物体的位置划分(找中位数使两边三角形数量近似) AVT Tree思想

伪代码

Intersect(Ray ray, BVH node) {
    if (ray misses node.bbox) return;

    if (node is a leaf node)
        test intersection with all objs;
        return closest intersection;

    hit1 = Intersect(ray, node.child1);
    hit2 = Intersect(ray, node.child2);

    return the closer of hit1, hit2;
}