Minimum Recolors to Get K Consecutive Black Blocks

Introduce

Well, this is my first leetcode-algo pratice totally in English, including question-comprehension, answer reference reading and personal answer recording. I have to admit that it’s a huge transition, which really differs from the old answering method I used in past times. And from now on, I will use this type to record my algo practice.Wish it would both help my comprehension to code-resolving and my english prononciation.

Overview

📖 Link: 2379. Minimum Recolors to Get K Consecutive Black Blocks

📆 Date: 2024-04-21 21:50

📋 Category: Single-Iteration / Sliding-Window

Description

You are given a 0-indexed string blocks of length n, where blocks[i] is either 'W' or 'B', representing the color of the ith block. The characters 'W' and 'B' denote the colors white and black, respectively.

You are also given an integer k, which is the desired number of consecutive black blocks.

In one operation, you can recolor a white block such that it becomes a black block.

Return the minimum number of operations needed such that there is at least one occurrence of k consecutive black blocks.

Example 1:

Input: blocks = "WBBWWBBWBW", k = 7
Output: 3
Explanation:
One way to achieve 7 consecutive black blocks is to recolor the 0th, 3rd, and 4th blocks
so that blocks = "BBBBBBBWBW". 
It can be shown that there is no way to achieve 7 consecutive black blocks in less than 3 operations.
Therefore, we return 3.

Example 2:

Input: blocks = "WBWBBBW", k = 2
Output: 0
Explanation:
No changes need to be made, since 2 consecutive black blocks already exist.
Therefore, we return 0.

Constraints:

• n == blocks.length
• 1 <= n <= 100
• blocks[i] is either 'W' or 'B'.
• 1 <= k <= n

Thoughts

💡 Actually the core idea is to find the minimum count of one specific in fixed array which actually comes from a string.

• ❎ Dynamic Planning? Probably not working, because with dp going on, we get both-growing k and blocks. We are not sure how to solidate just one variable.
• 🆗 Dual-Circulation: approachable, most ordinary solution, with O(n*k) time-complexity.
• 👍 Sliding-Window: because of the consecution, so it can presented as a sliding window.And maybe we can do something based on that...

Own Answer

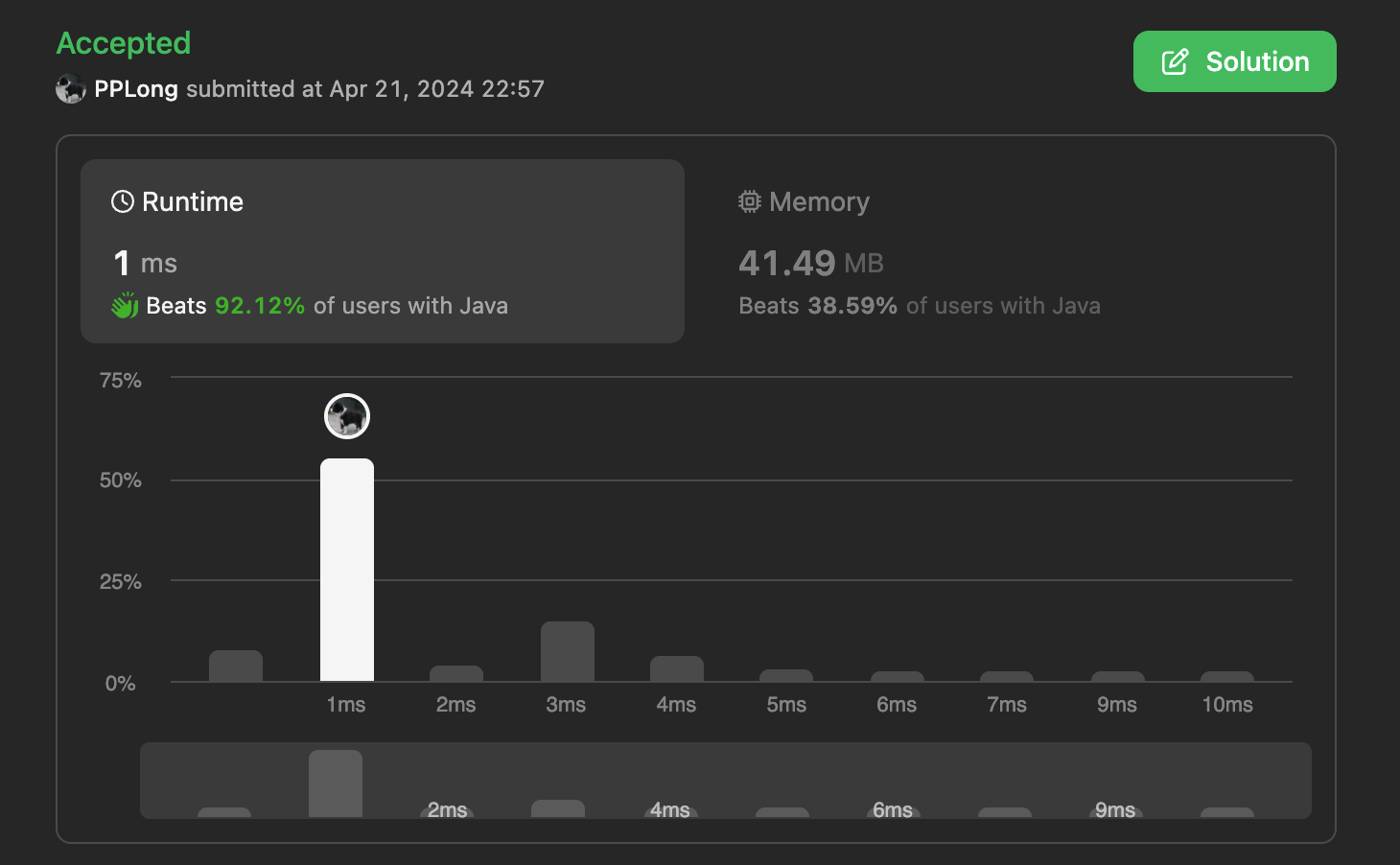
Dual-Circulation(N)

Thread

Linear and ordinary solution. Traverse the string array, for each element, count the numbers of M to consecutive next k-1 elements.And calculate the minimum record in this process.

$TimeComplexity=O((n-k+1)\ast k)$

class Solution {
    public int minimumRecolors(String blocks, int k) {
        int minWhiteBlockNums = Integer.MAX_VALUE;
        for (int i = 0; i <= blocks.length() - k; i++) {
            int currentWhiteBlockNums = 0;
            int j = 0;
            while (j < k) {
                if (blocks.charAt(i + j++) == 'W') {
                    currentWhiteBlockNums++;
                }
            }
            while (i + 1 < blocks.length() 
                && blocks.charAt(i) == 'B' && blocks.charAt(i + 1) == 'B') {
                i++;
            }
            minWhiteBlockNums = Math.min(minWhiteBlockNums, currentWhiteBlockNums);
        }
        return minWhiteBlockNums;
    }
}

Because it reaches O(n*k) time complexity, and has repeatedly calculate elements.So, it may not be the best solution.

Results-1

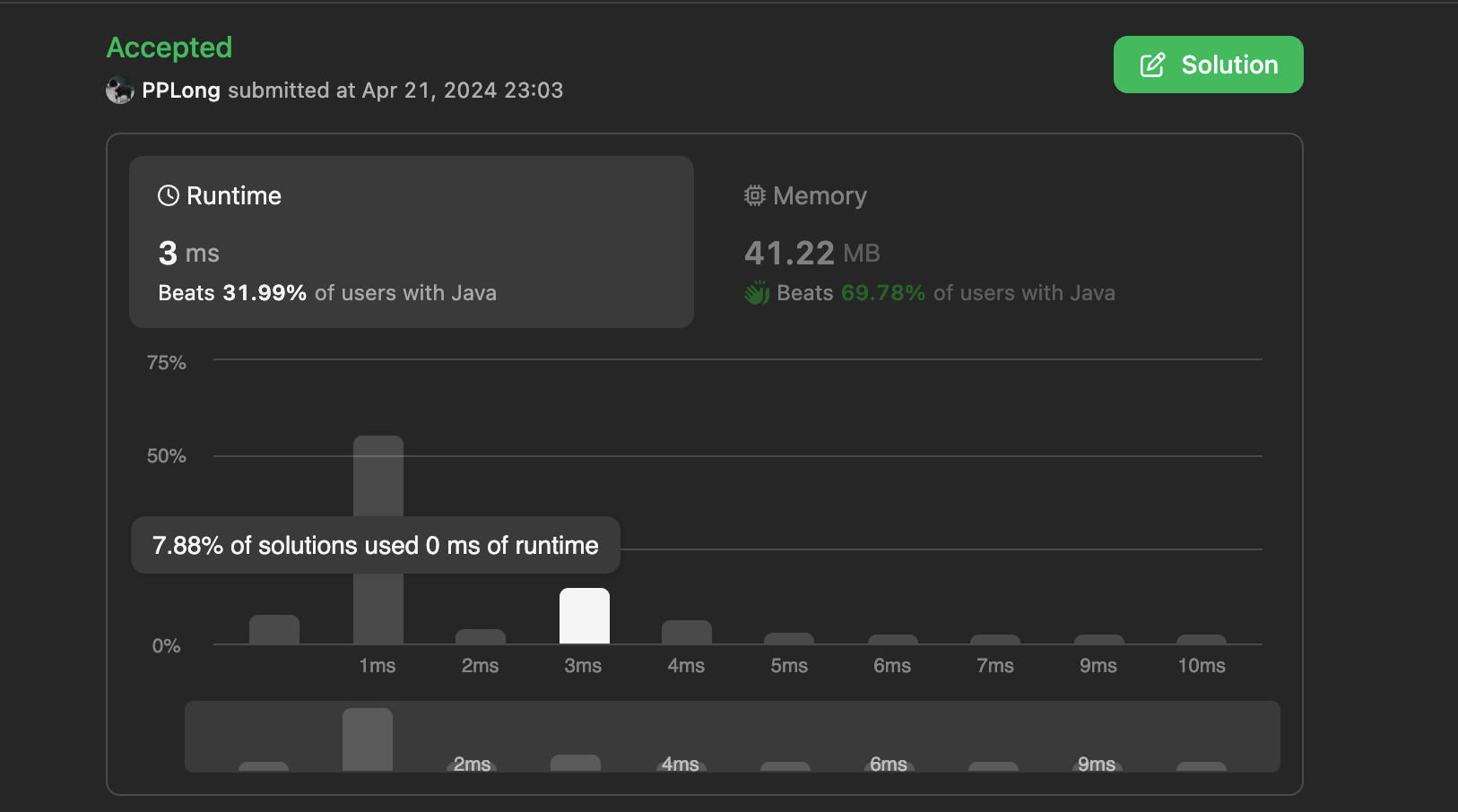
Sliding-Window

Thread

Because of its consecutiveness, we can see it is a unity of consecutive k elements as a sliding window, with each time moving a step forward. And it’s easy to simplify the problem because each step we just need to focus on changing status of the head and the tail. Calculating the difference, and we will get the answer in a more fast time complexity of O(n).

1. Calculate the count of W first k-elements
2. See the k-blocks as a sliding-window and simutate that the window move forwarding step by step
   1. If the character of new head is different from the old, then ...
   2. If the character of new tail is different from the old, then ...

$TimeComplexity=O(n-k+1)$

class Solution {
    public int minimumRecolors(String blocks, int k) {
        int minWhiteBlockNums = Integer.MAX_VALUE;
        int currentMin = 0;
        // calculate the size of 'W' in first k blocks
        for (int i = 0; i < k; i++) {
            if (blocks.charAt(i) == 'W') {
                currentMin++;
            }
        }
        minWhiteBlockNums = Math.min(currentMin, minWhiteBlockNums);
        for (int first = 1, tail = k; tail < blocks.length();first++, tail++) {
          	// run special logic for the head and tail
            if (blocks.charAt(first - 1) == 'W') {
                currentMin--;
            }
    
            if (blocks.charAt(tail) == 'W') {
                currentMin++;
            }
           minWhiteBlockNums = Math.min(currentMin, minWhiteBlockNums);
        }
        return minWhiteBlockNums;
    }
}