260. Single Number III

Info

🔗 ​https://leetcode.com/problems/single-number-iii/description/

Question

Given an integer array nums, in which exactly two elements appear only once and all the other elements appear exactly twice. Find the two elements that appear only once. You can return the answer in any order.

You must write an algorithm that runs in linear runtime complexity and uses only constant extra space.

Example 1:

Input: nums = [1,2,1,3,2,5]
Output: [3,5]
Explanation:  [5, 3] is also a valid answer.

Example 2:

Input: nums = [-1,0]
Output: [-1,0]

Example 3:

Input: nums = [0,1]
Output: [1,0]

Constraints:

• 2 <= nums.length <= 3 * 104
• -231 <= nums[i] <= 231 - 1
• Each integer in nums will appear twice, only two integers will appear once.

Thoughts

• Exactly two elements appear only once, other elements appear twice; array ---> One traversal is a better algorithm
• Consider algorithms with linear time complexity and constant space complexity
• Possible approach: hash
• Idea:
• Simple: brute force loop. Requires O(n^2) time complexity
• Advanced: Hash two outer loops, requires O(n) time complexity and O(n) space complexity
• Advanced: On space complexity, can't think of it...

Solution

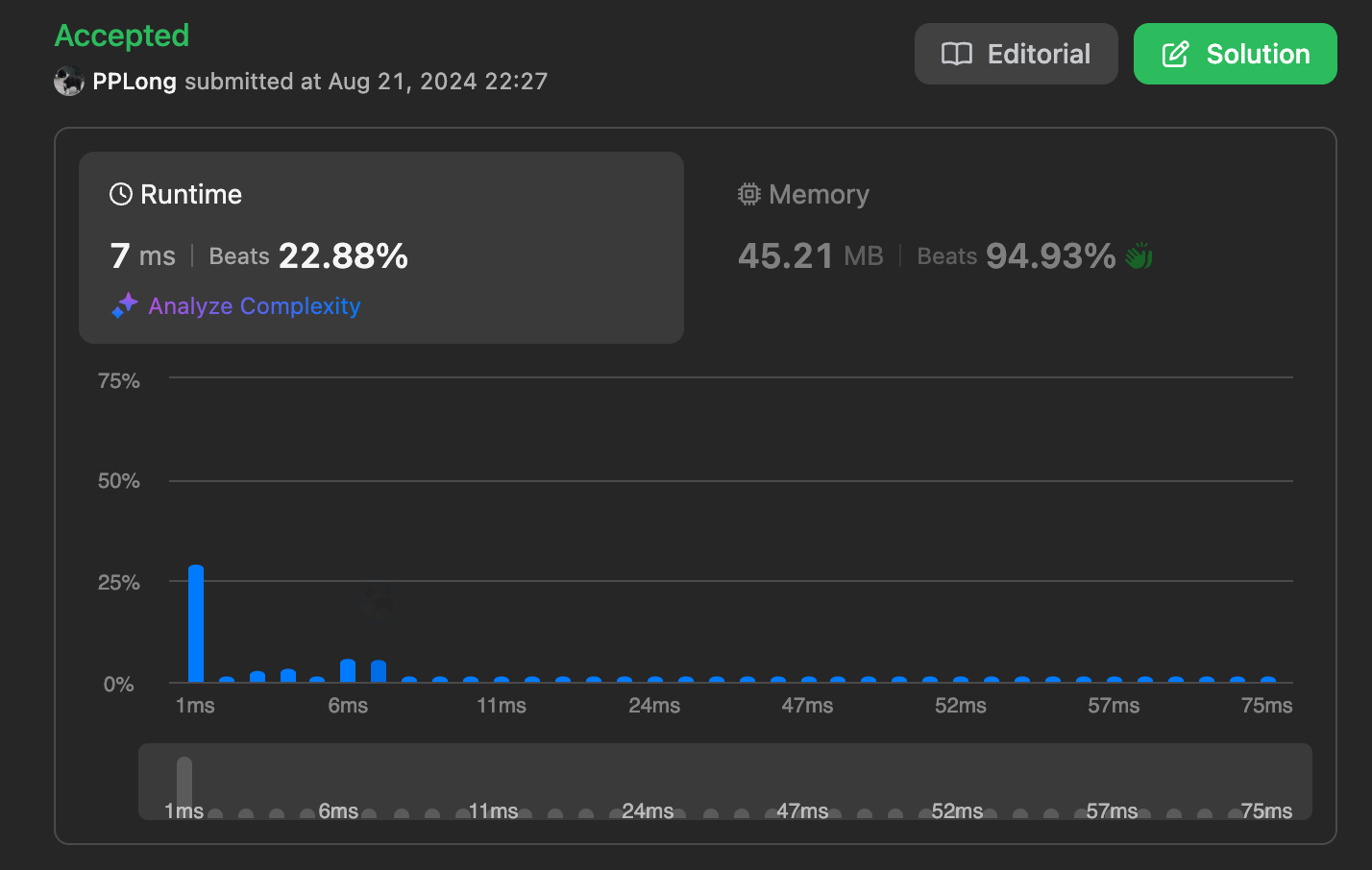
1. Hash

The first traversal fills in the value, the second traversal judges

public int[] singleNumber(int[] nums) {
        HashMap<Integer,Integer> map = new HashMap<>();
        int[] res = new int[2];
        for(int i = 0; i < nums.length; i++) {
            map.put(nums[i], map.getOrDefault(nums[i],0) + 1);
        }
        int index = 0;
        for(int i = 0; i < nums.length; i++) {
            if(map.get(nums[i]) == 1) {
                res[index] = nums[i];
                index++;
            }
        }
        return res;
    }

Result-1

2. Bit（Copy）

I forgot everything. I had done the same problem before, but I forgot it. It is quite skillful. An XOR formula explains everything:

$$a\oplus b\oplus a=b$$

XOR has commutative, associative, and reflexive laws

Idea: All XOR results are finally $a_1 \oplus a_2 $, which is definitely not equal to 0. Then traverse again, each time use nums[i] to do & operation, check whether it is == 1 (>0), if it is not equal to 0, then type1^=nums[i], and get a number of one type, if it is equal to 0, then type2 ^=nums[i], and get a number of another type.
The key is to understand that these two different numbers are assigned to two different classes through the & operation

class Solution {
    public int[] singleNumber(int[] nums) {
        int xorsum = 0;
        for (int num : nums) {
            xorsum ^= num;
        }
        // 防止溢出
        int lsb = (xorsum == Integer.MIN_VALUE ? xorsum : xorsum & (-xorsum));
        int type1 = 0, type2 = 0;
        for (int num : nums) {
            if ((num & lsb) != 0) {
                type1 ^= num;
            } else {
                type2 ^= num;
            }
        }
        return new int[]{type1, type2};
    }
}

// Author：LeetCode-Solution
// Linke：https://leetcode-cn.com/problems/single-number-iii/solution/zhi-chu-xian-yi-ci-de-shu-zi-iii-by-leet-4i8e/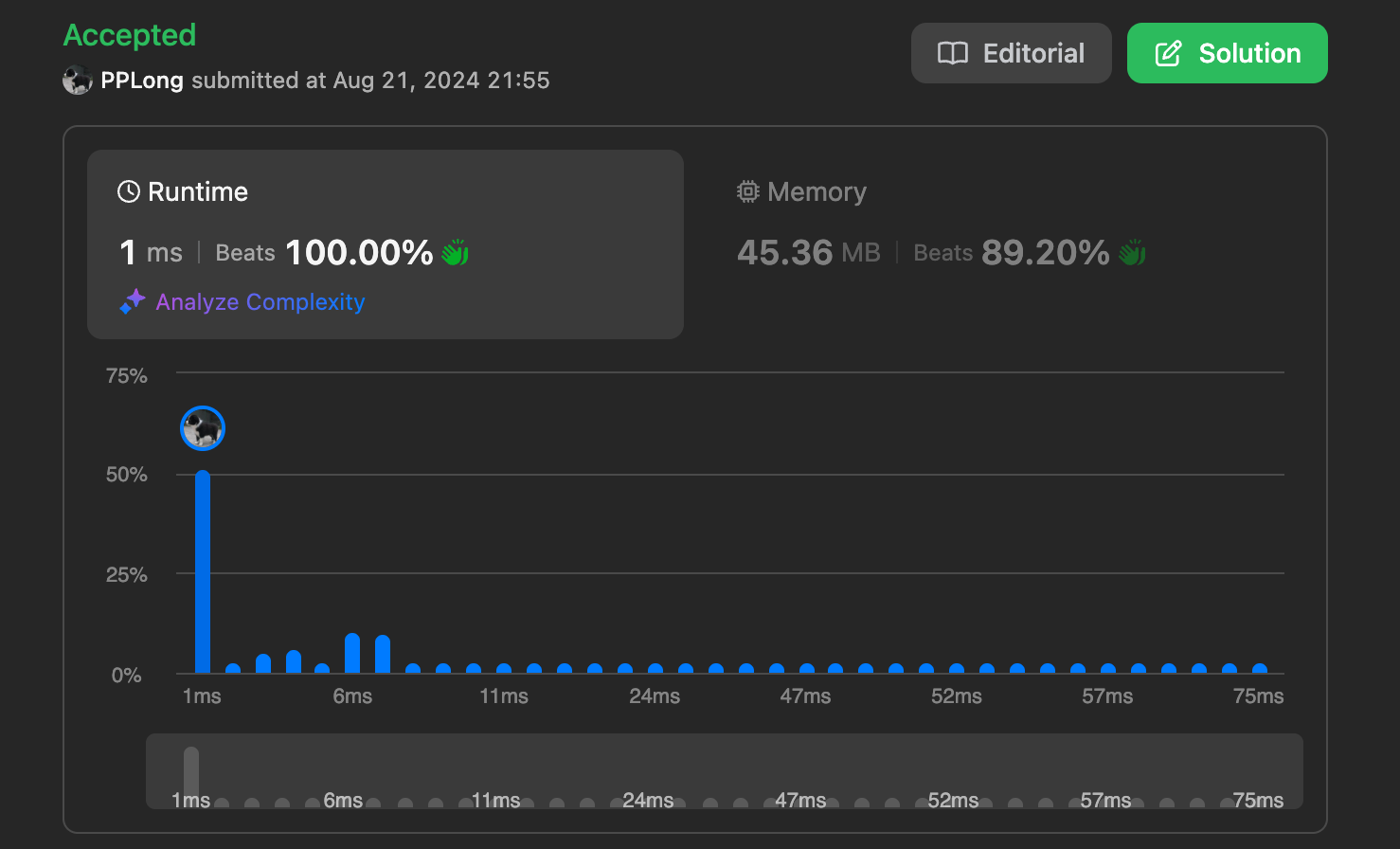

Result-2

Thinking

• The key is to think of XOR through two identical numbers. If you can't think of it, just send it directly...
• Think of basic methods when you are desperate. Here I have considered DP queue stack, but because there are too few conditions and the question is simple, I still can't think of a method. I also forgot the basic bit operations. Indeed, the fewer the conditions, the more you should consider.