Leetcode-373:Find K Pairs with Smallest Sums

PPLongAbout 4 min

Find K Pairs with Smallest Sums

Info

🔗 Leetcode-373. Find K Pairs with Smallest Sums

Description

You are given two integer arrays nums1 and nums2 sorted in non-decreasing order and an integer k.

Define a pair (u, v) which consists of one element from the first array and one element from the second array.

Return the k pairs (u1, v1), (u2, v2), ..., (uk, vk) with the smallest sums.

Example 1:

Input: nums1 = [1,7,11], nums2 = [2,4,6], k = 3
Output: [[1,2],[1,4],[1,6]]
Explanation: The first 3 pairs are returned from the sequence: [1,2],[1,4],[1,6],[7,2],[7,4],[11,2],[7,6],[11,4],[11,6]

Example 2:

Input: nums1 = [1,1,2], nums2 = [1,2,3], k = 2
Output: [[1,1],[1,1]]
Explanation: The first 2 pairs are returned from the sequence: [1,1],[1,1],[1,2],[2,1],[1,2],[2,2],[1,3],[1,3],[2,3]

Constraints:

1 <= nums1.length, nums2.length <= 105
-109 <= nums1[i], nums2[i] <= 109
nums1 and nums2 both are sorted in non-decreasing order.
1 <= k <= 104
k <= nums1.length * nums2.length

Thoughts

Precondition

Non-Decreasing Order: nums1 and nums2 both are sorted in non-decreasing order.`
1 <= k <= nums1.length * nums2.length

Thoughts

🆗 Violently Iterates: Viable but not recommend.
🤔 Binary Search?
🤔 Math Formula or Intuition? May work.
👍 Dynamic Programming? May work

Solution

Iterate (Optimized)

Seeing two index as (i, j), for already confirmed point, N(i) as the max selected j for current i, I , J as the collections of indexes of nums1 and nums2.

Core:Think of two logic intuitions:

Non-Decreasing Order: For m-th point, the point is: $(i, j) (\exists i \in I, j \in J, j = N (i) + 1)$

Optimize:

If (i, j) is not reached, then it will also not reach point (i + 1, j), as: $I_{i + 1} + J_{j} \geq I_{i} + J_{j}$

Logic Intuition

To better understand the possible point location, consider followed example.

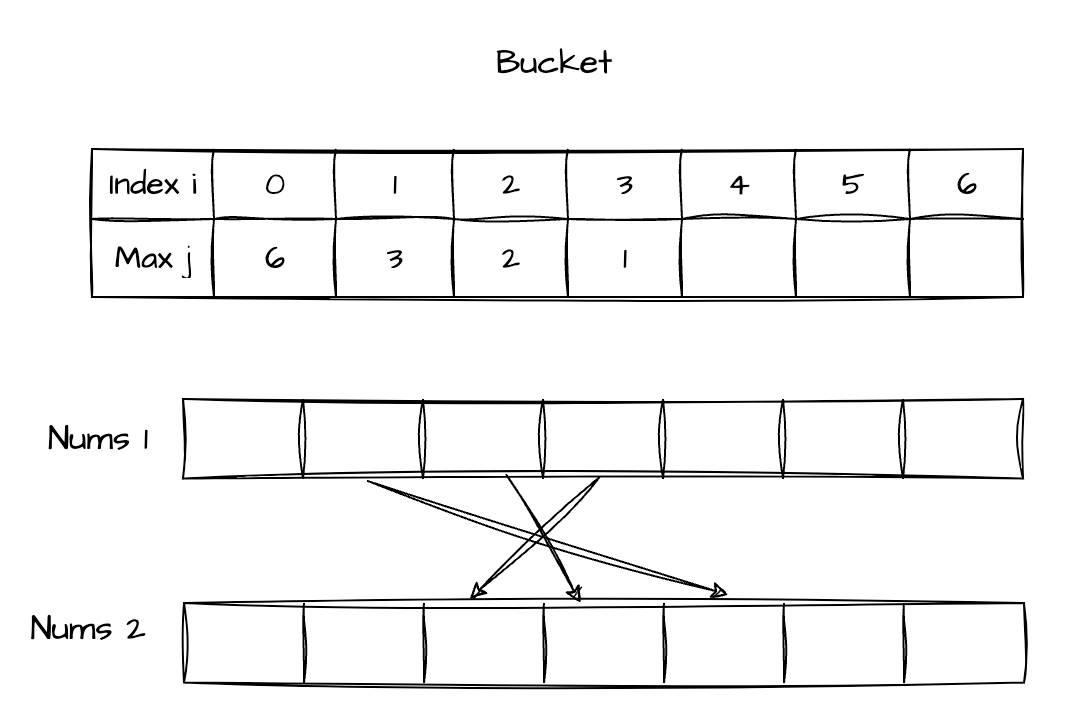
Step

Init buckets to hold the max selected j index for each i index.
Init the first point (0, 0)
For the rest, iterates the possible next point for each i index, followed by the logic above. Record the point which has minimum value and update the dp bucket. To the end...

class Solution {
    public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
        // Init default value of buckets
        int[] dp = new int[nums1.length];
        for (int i = 0; i < dp.length; i++) {
            dp[i] = -1;
        }
        // Init first element
        List<List<Integer>> res = new ArrayList<>();
        List<Integer> temp = new ArrayList<>();
        temp.add(nums1[0]);
        temp.add(nums2[0]);
        dp[0] = 0;
        res.add(temp);
        // Dynamic Programming
        for(int n = 1; n < k; n++) {
            temp = new ArrayList<>();
            int min = Integer.MAX_VALUE;
            int minI = 0;
            int minJ = 0;
            for (int i = 0; i < nums1.length; i++) {
                if (dp[i] < nums2.length - 1 && nums1[i] + nums2[dp[i] + 1] < min) {
                    min = nums1[i] + nums2[dp[i] + 1];
                    minI = i;
                    minJ = dp[i] + 1;
                }
                if (i - 1 > 0 && dp[i - 1] == -1) {
                    break;
                }
            }
            temp.add(nums1[minI]);
            temp.add(nums2[minJ]);
            res.add(temp);
            dp[minI] = minJ;
        }
        return res;
    }
}

Optimization

Pay attention to optimization here.

if (i - 1 > 0 && dp[i - 1] == -1) {
    break;
}

It reduces the unnecessary iteration for current point, because of intuition before: $I_{i + 1} + J_{j} \geq I_{i} + J_{j}$

Time Complexity: Unknown...

Space Complexity: Unknown...

Heap (Copy)

Core: Heap will auto-resort contained elements, so we just need to push candidate points to the heap, and just poll them.

Violent

Becasue unknown of selected the possible point, so we push all elements in the heap. And then, we just need to take the first k numbers

class Solution {
    public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
        int n = nums1.length, m = nums2.length;
        var ans = new ArrayList<List<Integer>>(k); // 预分配空间
        var pq = new PriorityQueue<int[]>((a, b) -> a[0] - b[0]);
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                pq.add(new int[]{nums1[i] + nums2[j], i, j});
            } 
        }
        int i = 0;
        while(i++ < k) {
            int[] p = pq.poll();
            ans.add(List.of(nums1[p[1]], nums2[p[2]]));
        }
        return ans;
    }
}

N: nums1.length
M: nums2.length

Time Complexity: $M a t h . m a x (O (N + M), O (K * L o g (N + M)))$

build the heap costs $(N + M)$
Poll one element from heap costs $L o g (N + M)$

Space Complexity: $O (N + M)$

Result: Overtime ❌

Optimize

The problem of Viloent Method is that we are unable to control which points to push. So we should try to do with that.\

Simulation

For the first, (0, 0), definitely push into heap. And we can poll it.
Next, we get choices,(0, 1) or (1, 0). So we just push both of them
Then, we get more choices
- if we poll (0, 1), then res is (0, 2) (1, 0)
- if we poll (1, 0), then res is (0, 1) (1, 1)
...
Converting to think reversely, if we got to push (i, j), then we have to poll (i - 1, j) or (i, j - 1). So we need to ensure that when we poll one of the two points, (i, j) will be pushed into the heap.

Note: There may have repeated points when doing that, because we will push (i, j) when polling (i - 1, j) and (i, j - 1)

So there should be some distinct-strategy

Distinct Strategy

Assume that

when polling (i, j - 1), push (i, j)
when polling (i - 1, j), do nothing

But this may induce new problem: if we just push (0,0) at first, we will only get (0, 1) (0, 2)... such points. Because we won’t push (i, j) when polling (i-1, j). So we have to handle this problem

Solution: push all the (i, 0) points at first.

Code

class Solution {
    public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
        int n = nums1.length, m = nums2.length;
        var ans = new ArrayList<List<Integer>>(k); // Pre assign space
        var pq = new PriorityQueue<int[]>((a, b) -> a[0] - b[0]);
        for (int i = 0; i < Math.min(n, k); i++) // Note range judge
            pq.add(new int[]{nums1[i] + nums2[0], i, 0});
        while (!pq.isEmpty() && ans.size() < k) {
            var p = pq.poll();
            int i = p[1], j = p[2];
            ans.add(List.of(nums1[i], nums2[j]));
          	// Note range judge
            if (j + 1 < m)
                pq.add(new int[]{nums1[i] + nums2[j + 1], i, j + 1});
        }
        return ans;
    }
}

// Author：灵茶山艾府
// Link：https://leetcode.cn/problems/find-k-pairs-with-smallest-sums/solutions/2286318/jiang-qing-chu-wei-shi-yao-yi-kai-shi-ya-i0dj/

Time Complexity $O (K * L o g (m i n (n, k)))$

each time cost $L o g (m i n (n, k))$ to push and poll element to heap.

Space Complexity $O (m i n (n, k))$

Summary

When dealing with sorting problem(eg, find the max k numbers...), we can think of the heap.