Exploring the Myers Algorithm
Exploring the Myers Algorithm
Preface
Recently, I have been trying to sort out the source code of ListAdapter under the androidx package to understand how it quickly identifies the differences between two lists, old and new. During this process, I encountered a particularly difficult and cumbersome code block, which I later learned was using the Myers comparison algorithm. This comparison code has also showcased its prowess in Git diff. Therefore, I wanted to carefully study the ideas behind this algorithm. After several weeks of delay, I finally started organizing my thoughts.
Introduction
What problem does the Myers Diff algorithm solve?
Introduction: It addresses the shortest path problem for converting between two strings.
Specifically: It can reveal the differences between two files from an algorithmic perspective.
Introduction
How to compare the differences between two files?
Every time a file is modified, the file system does not keep track of whether each line has changed; it only focuses on the entire file (otherwise, it would occupy a lot of extra space). For example, it is concerned with how file content A ultimately becomes content B, but it does not track how file content A transforms into B. Therefore, we cannot accurately know which lines we modified at that time; we only know when the file was updated and what it looks like afterward. Comparing lines can be simplified to string comparison, allowing us to reduce the problem to analyzing how to compare the differences between two strings.
How to compare the differences between two strings?
Concept Clarification
For strings, we need to clarify some concepts that may not be immediately necessary but should be understood.
Concept Clarification
- Input: String A is the input string, and string B is the target string that A needs to transform into using a specific set of instructions.
- SES: Shortest Edit Script, the algorithm finds the shortest edit script (understood as the least number of required instructions) to convert A into B. The instructions include:
- Deleting a character from A in sequence.
- Adding a character to B in sequence.
- LCS: Longest Common Subsequence, a sequence S that is a subsequence of two or more known sequences and is the longest among all such subsequences is called the longest common subsequence of the known sequences (I initially found this concept unclear and easily confused with the concept of Longest Common Substring).
Multiple Interpretations for One Transformation
For the following change, we can have different interpretations.
Original file: A B C A B B A
Modified: C B A B A C# Complete deletion, deleting first
-A -B -C -A -B -B -A +C +B +A +B +A +C# Complete deletion, deleting last
+C +B +A +B +A +C -A -B -C -A -B -B -A# Using A string as the main, modifying first
-A -B C -A B -B A +B +A +C# Following general convention
-A -B C -A B +A B -A +A +CFrom the above four different analyses, we can see that the modifications between the new and old files can be interpreted in various ways. But which one is better and aligns more with common understanding?
Typically, we prefer:
- Differences should manifest as more continuous additions or deletions, corresponding to changes in parts.
- Similar content should be maximized, meaning differences should be minimized.
- We prefer to see deletions rather than additions (as a convention).
How does Git implement the comparison of old and new version files?
When using Git, the git diff command allows us to quickly understand the differences between the current uncommitted changes and the committed version.
For example, if we create a file in a git repository containing ABCABBA (with a newline after each character), and after committing, we modify the original file to CBABAC (with a newline after each character), using the git diff command will yield the following result:
diff --git a/a.txt b/a.txt
index d8a1b05..5db0ef8 100644
--- a/a.txt
+++ b/a.txt
@@ -1,7 +1,6 @@
-A
-B
C
-A
B
+A
B
-A
\ No newline at end of file
+A
+C
\ No newline at end of file
(END)Viewing the commit differences in VsCode appears as follows:
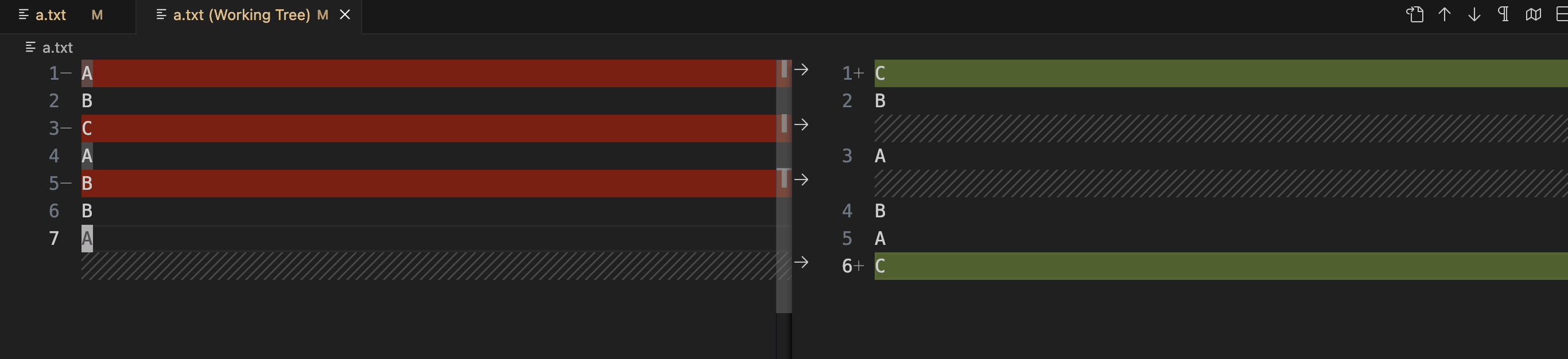
Does this align with our expected modification predictions? How does Git achieve this?
git diff has four built-in algorithms, including myers (default), minimal (attempts to find the smallest difference), patience, and histogram, as shown in the following image.
Introduction
📖 Git - diff-options Documentation
--diff-algorithm={patience|minimal|histogram|myers}
Choose a diff algorithm. The variants are as follows:
default,myersThe basic greedy diff algorithm. Currently, this is the default.
minimalSpend extra time to ensure the smallest possible diff is produced.
patienceUse "patience diff" algorithm when generating patches.
histogramThis algorithm extends the patience algorithm to "support low-occurrence common elements".
For instance, if you configured the diff.algorithm variable to a non-default value and want to use the default one, then you have to use the --diff-algorithm=default option.
It can be seen that the default method for calculating differences is through the myers algorithm, which brings us to our main topic.
Reasoning
Rule Definition
How to transform string A into string B? Understanding this process must be combined with the perspective of file changes.
First, we hope for minimal changes and concentration of changes, so we need to consider the cost of transforming A into B. The known minimal change types are: deletion, addition, and no change. No change incurs no cost, while deleting or adding a character is assumed to have a cost of 1, meaning they have the same cost weight. To achieve the desired transformation reasoning, the following logic must be followed:
- When no change can be maintained, prioritize maintaining no change.
- First, check if the transformation can be achieved through deletion.
- Use the solution with the least cost.
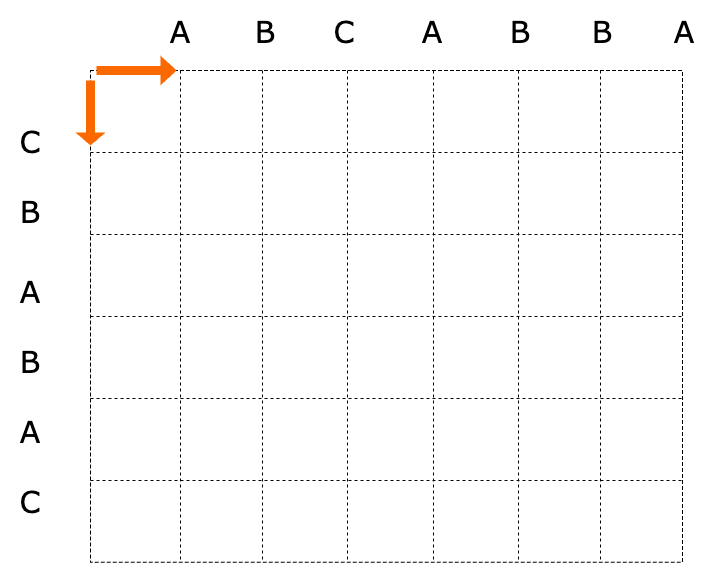
Using a well-known example: string A (A B C A B B A) and string B (C B A B A C), we can create a diagram as follows:
- The horizontal axis represents string A, and the vertical axis represents string B.
- Moving one space to the right represents deleting the character at the arrow, while moving one space down represents adding the character at the arrow.
- Each actual change with cost is called a step, and moving right or down requires one step.
- When the next horizontal coordinate character matches the vertical coordinate character, diagonal movement is allowed, and this solution is prioritized, incurring no steps (representing the actual meaning of no change).
- Prefer to move right (by convention, deletion is prioritized).
- Finally, reaching the bottom right corner indicates the transformation is complete.
The core idea is similar to greedy + pointer-based traversal, using string A as the original string and the distance between characters as index elements (similar to the thin vertical pointer | shown when typing in an input box), starting from 0 to perform the above three operations based on the new string, ultimately transforming it into the new string.
Manual Simulation
Let's try to perform the above example manually, assuming we are the computer and can only perform single-step operations. How can we achieve the correct result?
Step One
The original string is ABCABBA.
- Try deleting the character A --> |BCABBA (| the string before indicates it has been validated, matching the prefix of C, while the string after indicates it has not been validated and belongs to A, still unvalidated)
- Try adding the character C --> C|ABCABBA
Step Two
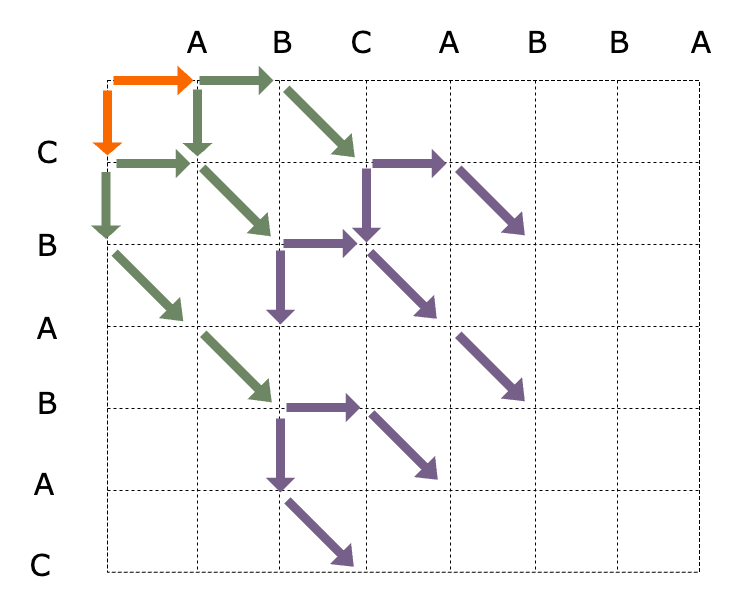
- |BCABBA
- Try deleting the character B --> |CABBA --> diagonal match --> C|ABBA
- Try adding the character C --> |CBCABBA --> diagonal match --> C|BCABBA
- C‘ABCABBA
- Try deleting the character A --> C|BCABBA --> diagonal match --> CB|CABBA
- Try adding the character B --> CB|ABCABBA --> diagonal match --> CBA|BCABBA --> CBAB|CABBA
.png)
Step Three
Similar to the above process, please deduce on your own.
Step Four
Similar to the above process, please deduce on your own.

Step Five
Similar to the above process, please deduce on your own.

Summary
In summary, its core idea is similar to greedy + pointer-based traversal, using string A as the original string and the distance between characters as index elements (similar to the thin vertical pointer | shown when typing in an input box), starting from 0 to perform the above three operations based on the new string, ultimately transforming it into the new string.
Reflection
Why consider moving diagonally here without considering the next step before moving diagonally?
K-Line
Here, the k-line is defined as the line represented by k = x - y, which can be expressed in the following form.
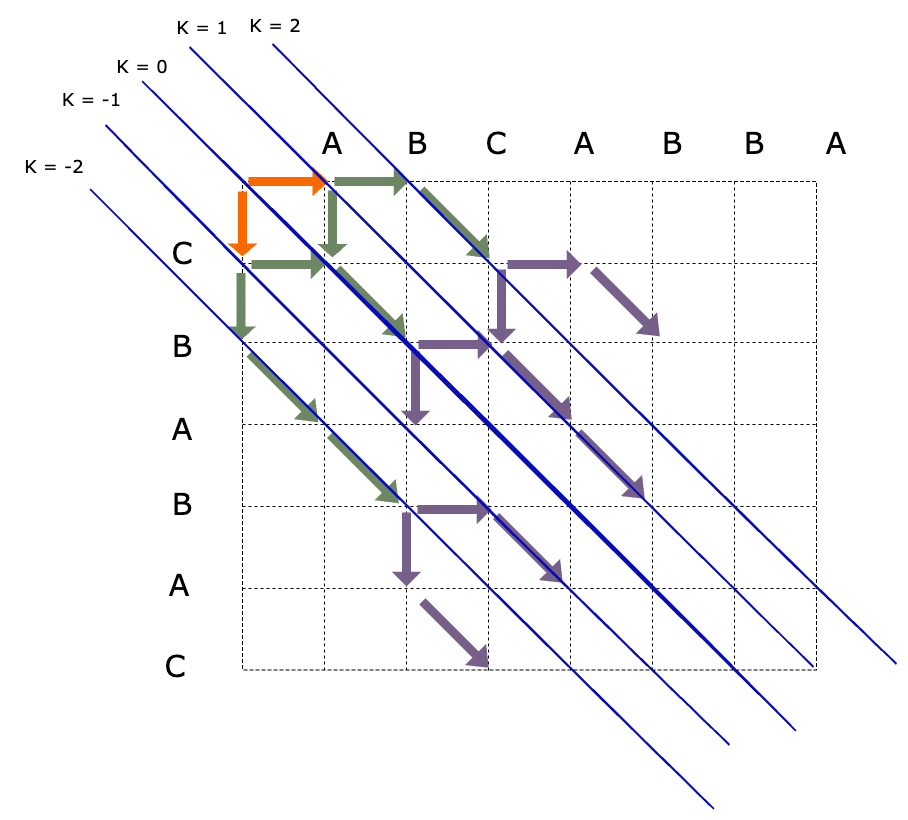
How does introducing the K-line help in understanding the Myers algorithm?
Using adjacent K-lines restricts the range of movement for one step in advance.
For example, starting from the (x, y) point on the current k-line, since movement can only be to the right or down, the next step’s k-line can only be k + 1 or k - 1. Therefore, this way, the originally uncertain values for one step can be locked to points that must be on one of the two lines.
Theorem about K-lines
- For a path with a step length of D, the value range of the k-line at the endpoint must be within the following interval: $ K \in { -D, \ -(D-2), \ \dots, \ 0, \dots , \ D-2, \ D } $
- Paths with even step lengths fall on even k-lines, while paths with odd step lengths fall on odd k-lines.
- For a point on a k-line, the previous point can only be reached by one of the following two methods:
- Moving down from a point on the K+1 line.
- Moving right from a point on the K-1 line.
Thought Process
Based on the greedy algorithm, the following simulation can be conducted:
Assess all possible K-line movement scenarios for each step, checking whether it can reach the endpoint, and recording the farthest point on each K-line for each step.
- For a point with D steps, if the current k-line value is K.
- Determine how the previous point (the last landing point) moved to this point (down or right).
- Derive the previous point's k-line and deduce the coordinates of the previous point based on the historical farthest points of each k-line.
- Derive the coordinates of this point.
- Check if this point can still move diagonally.
- Record the farthest point reached on that K-line.
- Check if the endpoint is reached; if so, deduce, otherwise loop back.
Code
Based on the above analysis, the following code is provided.
Path Searching
First, we need to find a path that satisfies the above conditions.
/**
* Find the minimum number of steps needed to convert string A to string B
* @param a Original string
* @param b New string/**
* @return A hash table of the farthest X coordinate points reached by all K lines at each step
*/
fun findMinStepPath(a: String, b: String): List<Map<Int, Int>> {
// Maximum number of steps needed
val maxStep = a.length + b.length
// Store the farthest x value reachable by the current K line
val v = mutableMapOf<Int, Int>()
// Save the farthest x value each K line can reach at each step
val list = mutableListOf<Map<Int, Int>>()
list.add(mapOf(Pair(0, 0)))
// Greedy algorithm, sequentially observe the process of each step
outerLoop@for (d in 1..maxStep) {
// The farthest x value each K line can reach at the current step
val tempV = mutableMapOf<Int, Int>()
// Iterate through all possible K line points at the current step
for (k in -d..d step 2) {
/*
* Important condition: For the current step and current point on the K line, determine how the previous point moved to this point (can only be right or down)
* 1. Special case -- down: The current point's K line is already -d (derived from the formula's constraints, obtained by moving from the k-1 line down)
* 2. Special case -- up: The current point's K line is already d (derived from the formula's constraints, obtained by moving from the k-1 line right)
* 3. General case:
* 1. Down: The farthest x value reachable by the k+1 line is greater than that of the k-1 line (can be understood as the k+1 line's path deleted more characters, which is the desired outcome)
* 2. Up: Conversely
*/
val isDown = k == -d || k != d && v.getOrDefault(k + 1, 0 ) > v.getOrDefault(k - 1, 0)
// Derive the K line and coordinate of the previous step
val prevK = if (isDown) k + 1 else k - 1
val prevX = v.getOrDefault(prevK, 0)
// Derive this step's coordinate from the previous K line and coordinate
var x = if (isDown) prevX else prevX + 1
// Check if diagonal movement is still possible
while (x < a.length && x - k < b.length && a[x] == b[x - k]) {
x++
}
// Count the farthest coordinate point reachable by this K line at this step
v[k] = x
tempV[k] = x
// If matching is complete, i.e., reaching the bottom right endpoint, exit
if (x == a.length && x - k == b.length) {
list.add(tempV)
break@outerLoop
}
}
// Save the farthest points of each K line at each step
list.add(tempV)
}
return list
}Path Backtracking
First, understand the data structures needed for backtracking
data class Point(
val x: Int,
val y: Int
) {
override fun toString(): String {
return "Point(x=$x, y=$y)"
}
}
data class Snake(
val startPoint: Point,
val midPoint: Point?,
val endPoint: Point,
val isDown: Boolean
) {
override fun toString(): String {
return "Snake(startPoint=$startPoint, isDown=${if(isDown) "|" else "->" } midPoint=$midPoint, endPoint=$endPoint)"
}
}Understand Snake
A Snake represents a simplified representation of each step's path, containing the coordinates of Start Point -- Mid Point -- End Point to indicate the path taken in that step.
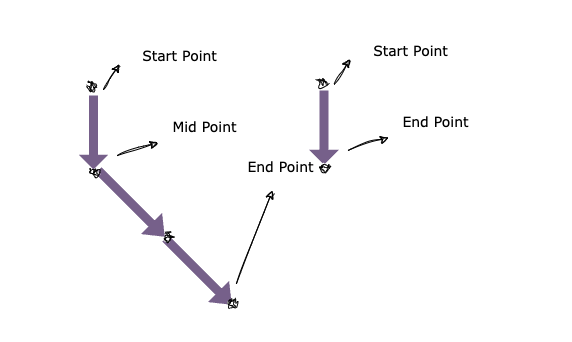
Specific backtracking code:
/**
* Backtrack to derive the original path from the original string to the new string
* @param a Original string
* @param b New string
* @param list The hash table of the farthest X coordinate points reached by all K lines at each step
* @return A list containing the movement information of each step
*/
fun trackPathBack(a: String, b: String, list: List<Map<Int, Int>>): Deque<Snake> {
var currentX = a.length
var currentY = b.length
// The actual list contains the K line path of step 0, so need to subtract 1
var currentD = list.size - 1
val snakes = LinkedList<Snake>()
/*
* If the current point is obtained from the fifth step, then we need to backtrack to the K line-X coordinate situation at the fourth step for judgment
* Determine how the previous point moved to this point (can be understood as scene restoration)
*/
// Understand that here we first perform a decrement
while (--currentD >= 0) {
// Calculate the K line of the current point
val k = currentX - currentY
val startX = currentX
val startY = currentY
val v = list[currentD]
// Scene recreation
val isDown = k == -currentD || k != currentD && v.getOrDefault(k + 1, 0 ) > v.getOrDefault(k - 1, 0)
// Derive the K line and coordinate of the previous step
val prevK = if (isDown) k + 1 else k - 1
val prevStartX = v.getOrDefault(prevK, 0)
val prevStartY = prevStartX - prevK
// Derive the mid coordinate (i.e., the coordinate before the diagonal line; if not moving diagonally, there is no mid coordinate)
val midX = if (isDown) prevStartX else prevStartX + 1
val midY = midX - k
currentX = prevStartX
currentY = prevStartY
// Push onto the stack
snakes.push(
Snake(
Point(currentX, currentY),
if (midX != startX || midY != startY) Point(midX, midY) else null,
Point(startX, startY),
isDown
)
)
}
return snakes
}Application
With the path experienced at each step, it is straightforward to derive the transformation process from string A to string B.
/**
* Get a Git-like add and remove change prompt
*/
fun getDiffTextBySnakes(a: String, b: String, snakes: Deque<Snake>): String {
var x = 0
var y = 0
val res = StringBuilder()
while(snakes.isNotEmpty()) {
val snake = snakes.pop()
println(snake.toString())
val str: String
if (snake.isDown) {
// Add characters from the new string
str = "+${b[y++]} "
} else {
// Remove characters from the original string
str = "-${a[x++]} "
}
res.append(str)
// If a diagonal has been passed, it means some characters remain unchanged, requiring additional processing
if (snake.midPoint != null) {
var diff = snake.endPoint.x - snake.midPoint.x
while(diff-- > 0) {
res.append("${a[x++]} ")
// Note that y also needs to increment
y++
}
}
}
return res.toString()
}The above method has the following invocation:
fun main() {
val a = "ABCABBA"
val b = "CBABAC"
val list = MyersAlgo.findMinStepPath("ABCABBA", "CBABAC")
val snakes = MyersAlgo.trackPathBack(a, b, list)
val diffStr = MyersAlgo.getDiffTextBySnakes(a, b, snakes)
println(diffStr)
}The following result is produced:
Snake(startPoint=Point(x=0, y=0), isDown=-> midPoint=null, endPoint=Point(x=1, y=0))
Snake(startPoint=Point(x=1, y=0), isDown=-> midPoint=Point(x=2, y=0), endPoint=Point(x=3, y=1))
Snake(startPoint=Point(x=3, y=1), isDown=| midPoint=Point(x=3, y=2), endPoint=Point(x=5, y=4))
Snake(startPoint=Point(x=5, y=4), isDown=-> midPoint=Point(x=6, y=4), endPoint=Point(x=7, y=5))
Snake(startPoint=Point(x=7, y=5), isDown=| midPoint=null, endPoint=Point(x=7, y=6))
-A -B C +B A B -B A +C